Информационный бюллетень
ракетных войск

Выбор точек прицеливания при пусках баллистических ракет по неоднородным целям.

Москва, 1961

CIA USA 1962

Перевод с английского © А.Королёв, 2018

Наш адрес: ruzhany@narod.ru

Из рассекреченных документов ЦРУ.

ОГЛАВЛЕНИЕ

    Несколько слов от автора сайта

Некоторые вопросы маскировки основных позиционных районов ракетных войск

1. Краткое описание современных средств разведки

2. Основные цели и задачи выполнения оперативной и войсковой маскировки объектов ракетных войск

3. Основные методы войсковой маскировки структур и боевой техники ракетных войск

4. Некоторые вопросы организации работ

Смотри также:

Полковник Пеньковский: Архивные документы разведки США

Подготовка к боевым действиям полка, вооруженного ракетами Р-12

Выбор точек прицеливания при пусках баллистических ракет по неоднородным целям

Организация боевого обеспечения полка вооруженного стратегическими ракетами

Создание учебной материальной базы для специальной подготовки в ракетных полках

Из опыта организации и проведения учений по специальной подготовке офицерского состава ремонтно-технической базы на этапе формирования

Планирование и организация боевой подготовки в штабах и подразделениях ракетных войск в учебный период

Некоторые вопросы маскировки основных позиционных районов ракетных войск

Ракетный комплекс средней дальности 8П763 и 8П863 с БРСД Р-12 (8К63), Р-12У (8К63У), SS-4, Sandal

Несколько слов от автора сайта

Продолжаем выкладывать материалы, переданные полковником Пеньковским западным разведкам и имеющие отношение к Ракетным войскам.

И еще одна статья из 2-го выпуска «Информационного бюллетеня ракетных войск»

В настоящее время английскую версию статьи можно найти на сайте ЦРУ в виде нескольких сохраненных и рассекреченных копий:

— Strategic Missile Bulletin: The Selection of Aiming Points in Firings of Ballistic Missiles at Heterogeneous Targets. [Рассекречен 13 января 2012 года]

В очередной раз предупреждаю:

К сожалению, оригинальная статья на русском языке до сего времени недоступна. Данная публикация является «обратным переводом» рассекреченного документа ЦРУ.

Естественно, при переводе я мог допустить ошибки, и не только в терминологии...

Выбор точек прицеливания при пусках баллистических ракет по неоднородным целям

1. Краткое описание современных средств разведки.

Так как положение точки прицеливания в значительной степени влияет на результат стрельбы, выбор точек прицеливания является очень важной задачей при планировании ракетных стрельб. Под точкой прицеливания понимается точка, для которой подготовлены данные для запуска ракет. Мало того, что ожидаемый результат снижается, если точка прицеливания (точки) неправильно вычислена, но и заданная степень поражения цели может быть не достигнута, несмотря на достаточную величину заряда (зарядов).

Точное решение задачи выбора точек прицеливания затруднено и может быть достигнуто с помощью электронных вычислительных машин. В то же время можно использовать методы аппроксимации при выборе точек прицеливания, которые позволяют быстро и просто определить местоположение, близкое к оптимальному, и гарантировать с достаточной точностью на практике решение рассматриваемой задачи.

Метод выбора точек прицеливания зависит от характера цели. Все стратегические цели можно разделить на две основные группы, в соответствии с их характером.

В первую группу входят такие объекты, как политико-административные центры, многие военно-промышленные районы, районы базирования войск и другие. Характерной особенностью этой группы является то, что отдельные части, составляющие цель (здания, технические сооружения и т. д.), равномерно расположены по всей территории цели и примерно одинаковы по своим существенным признакам. Такие цели обычно известны как площадные цели.

Вторая группа состоит из групповых разнородных целей. К ним относятся средства ядерного нападения (ракетные и авиационные базы), некоторые военно-промышленные районы и другие. Эти цели состоят из ограниченного числа независимых целей (частей), распределенных случайным образом по всей территории цели и отличающихся как по своим существенным характеристикам, так и по важности.

Задача выбора точек прицеливания для стрельб по целям во второй группе сложнее, так как в этом случае необходимо учитывать не только взаимное расположение объектов, составляющих цель, но и их разную уязвимость к эффектам поражающих факторов взрыва. В настоящей статье изучается решение этой задачи методом аппроксимации. Выбор точек прицеливания для площадной цели указан в правилах стрельбы.

При выборе точек прицеливания следует начинать с уверенности в выполнении планируемой огневой задачи и необходимости обеспечения максимальной экономии при стрельбе. В качестве надежности выполнения огневой задачи, принимаем вероятность поражения цели — Р, а в качестве характеристики экономии пусков — показатель экономии использования зарядов — W, определяемый по формуле

где M [ξ] — математическое ожидание ущерба, нанесенного цели; ξ_max - максимально возможный ущерб для данной цели.

Из формулы (1) видно, что наибольшая экономия при стрельбе будет в случае, когда математическое ожидание поражения, нанесенного цели, равно M [ξ] или, что то же самое, когда математическое ожидание поражения часть цели — M, достигает максимального значения. Здесь примем, что пораженная часть цели выражается в процентах от общего количества частей (установок), составляющих цель.

Вероятность поражения групповой цели P можно связать с вероятностью поражения каждой отдельной части цели Pi. При выполнении задачи необходимо начать с обеспечения необходимой вероятности поражения каждой отдельной части цели. Вопрос об определении этой вероятности, который вытекает из степени зависимости выполнения огневой миссии, будет рассмотрен ниже. Пока мы будем предполагать, что имеем значение необходимой вероятности поражения для каждой отдельной части цели. Задача выбора точки прицеливания (точек) может быть сформулирована следующим образом:

Даны: цель, тротиловый эквивалент ядерного заряда, вероятности рассеивания по дальности (Вд) и бокового рассеивания (Вб), а также требуемая вероятность поражения каждой части (установки) цели. Определение точки прицеливания (или точек в случае нескольких стрельб) исходит из выполнения двух условий:

1. Вероятность поражения каждой части должна быть не меньше требуемой,
P_i ≥ P_{i тр};

2. Математическое ожидание поражения части цели должно быть максимальным,
M = M max.

Для решения этой задачи предлагается графический метод, суть которого заключается в следующем. По графическому макету плана цели находим область, в которой каждая точка, если она выбрана в качестве точки прицеливания, гарантирует, что вероятность поражения каждой части цели не меньше требуемой (первое условие). Затем в пределах выбранной области берется точка, которая обеспечивает выполнение второго условия, которое дает максимальное значение математической вероятности поражения части цели. Эта точка рассматривается как цель.

Давайте рассмотрим принцип графического макета.

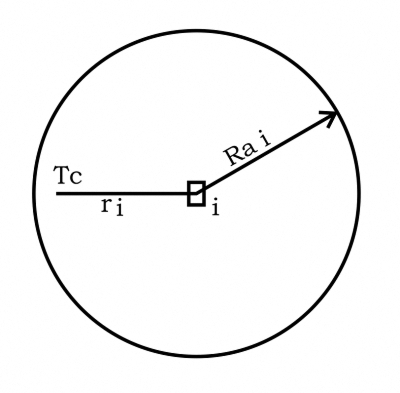
Вероятность поражения i-й части цели определяется как вероятность попадания точек в границы зоны поражения. Это зависит от дальностных и боковых характеристик рассеивания от радиуса зоны поражения для i-й части R_{a i} и от смещения точки прицеливания Тс по отношению к i-й части к r_i (рис. 1), Эллипс рассеивания для баллистических ракет может быть заменен без серьезного ущерба кругом с характеристиками

Тогда вероятность поражения i-й части P_i зависит от трех значений R_{a i}, Вп и r_i. Если мы знаем P_i, Вп и R_{a i}, мы можем определить r_i — то есть максимальное расстояние между точкой прицеливания и частью цели, при котором мы все равно будем иметь необходимое значение вероятности поражения цели.

Ясно, что если окружность с радиусом r_i начерчена из центра части цели, мы имеем область, в пределах которой вероятность поражения части цели P_i для любой точки не меньше требуемой, т.е. мы имеем зону в которой выполняется первое условие для i-й части:

P_i >> P_{i тр};

если r_i определялось исходя из требуемой вероятности поражения части цели.

{Рисунок 1}

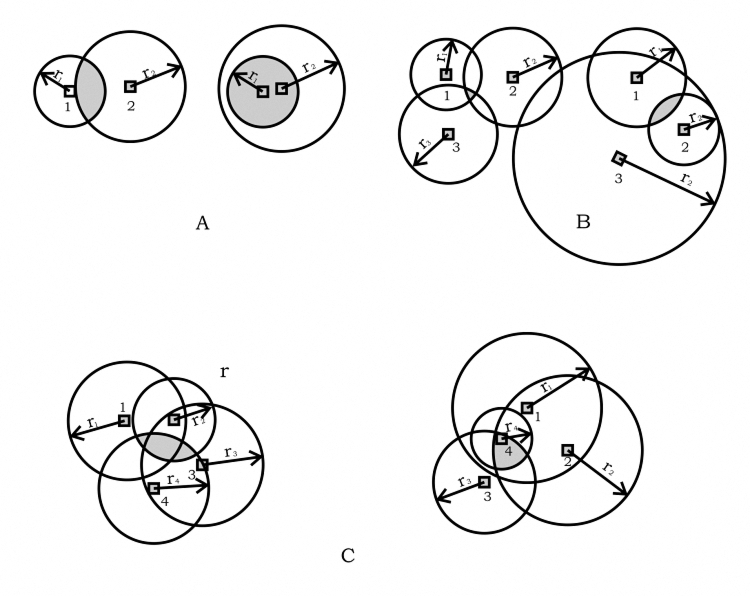
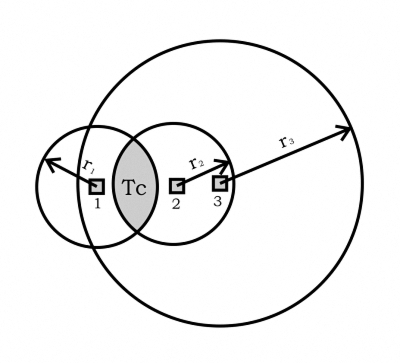
Определив r_i для каждой части цели и начертив на плане цели соответствующие круги из центра каждой части, в пространстве, перекрываемом всеми кругами, мы получим область, в которой выполняется первое условие для всех частей цели. На рисунке 2 показаны примеры такого макета для целей, состоящих из двух, трех и четырех частей (мы получаем аналогичную картину для большего количества частей).

{Рисунок 2}

Конкретные условия могут привести к случаю, когда общая площадь сформирована не для всех частей. Это означает, что при запуске одиночной ракеты с зарядом данного тротилового эквивалента требуемая степень поражения не обеспечивается. Следовательно, необходимо либо увеличить величину заряда, либо запланировать запуск нескольких ракет. В последнем случае необходимо определить необходимое количество ракет. Для этого все части цели делятся на минимальное количество групп, таким образом, что для каждой группы существует одна общая область возможных точек прицеливания. Расход ракет устанавливаются в соответствии с количеством таких групп. Точки прицеливания в этом случае выбираются для каждой отдельной группы частей в соответствии с расходом ракет.

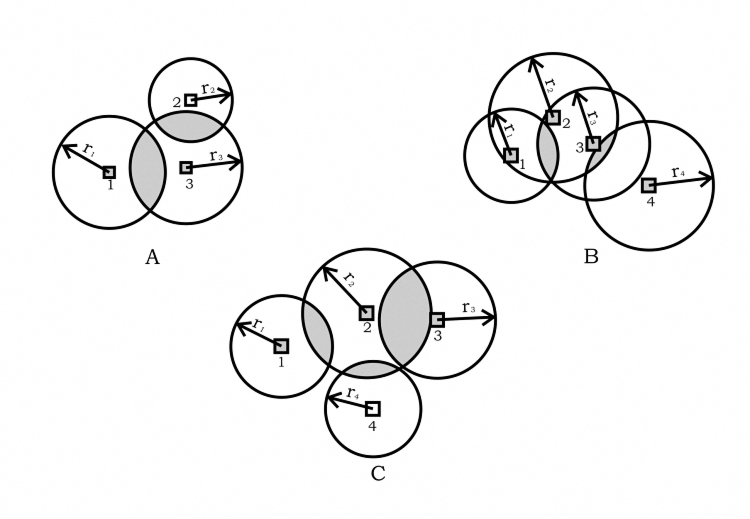
Примеры целей, состоящие из трех и четырех частей, показаны на рисунке 3. Очевидно, что в случаях, представленных на рисунках 3a и 3b, необходимы две ракеты, а на 3c - три ракеты. Аналогичная ситуация может возникнуть, когда цель состоит из большего количества частей (установок). Однако следует отметить, что на практике количество групп частей и, следовательно, расходование ракет не будет превышать двух или трех, максимум четырех, поскольку радиусы зон поражения являются большими и отличаются незначительно от возможных расстояний между различными частями цели.

{Рисунок 3}

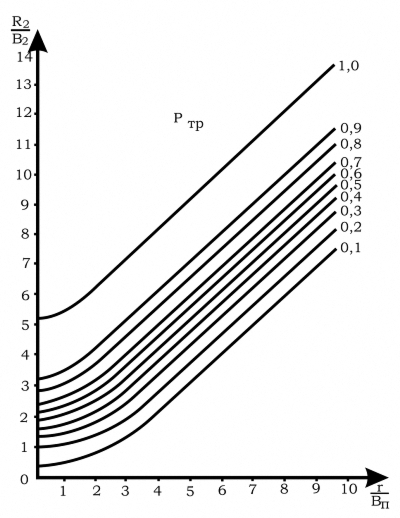
Наиболее удобно определить значение r_i по графику (рис. 4). Исходными параметрами будут: необходимая вероятность поражения цели P_{i тр} и радиус зоны поражения i-й части R_{a i}, выраженный в единицах Вп. При чтении графика значение r_{В i} также будет выражено в единицах Вп. Для определения r_i необходимо умножить r_{В i} на Вп, т. е.

r_i = r_{В i} Вп. (3)

Таким образом, после определения r_i для каждой части цели определяется область возможных положений для точки (точек) прицеливания, в которой обеспечивается заданная вероятность выполнения запланированной огневой задачи. Затем необходимо в пределах найденной области выбрать оптимальную точку прицеливания, обеспечивающую максимальное математическое ожидание поражения части цели.

Математическое ожидание поражаемой части цели (в рассматриваемой задаче это будет математическое ожидание количества пораженных частей цели) можно определить как сумму вероятностей поражения частей цели, деленную на общее количество частей:

где, n - количество частей;

P_i - вероятность поражения i-й части.

Следовательно, необходимо найти точку, в которой сумма вероятностей поражения отдельных частей будет максимальной.

{Рисунок 4}

Вначале рассмотрим цель, состоящую из двух частей (рис. 5), и предположим, что точка прицеливания Тс выбрана в центре области возможных мест точек прицеливания. Очевидно, что, перемещая точку прицеливания к одной из частей, например, первому, вероятность поражения первой части возрастает, а второго уменьшается.

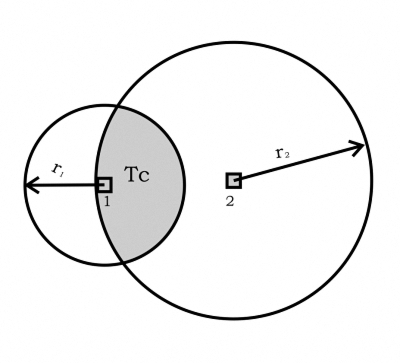{Рисунок 5}

На рисунке 6 графически показано изменение вероятности поражения с увеличением расстояния между частями цели и точкой прицеливания. Из графика ясно, что если начальная вероятность (в центре области) больше 0,5, то, уменьшая рассматриваемое расстояние до определенной величины, вероятность увеличивается в меньшей степени, чем уменьшается при увеличении расстояния между точкой прицеливания и частями на одну и ту же величину. Фактически, с начальной вероятностью 0,7, перемещая точку прицеливания к части на один Вп, вероятность поражения увеличивается на 0,17, как видно из графика; но, перемещая точку прицеливания на один Вп - она уменьшается на 0,30.

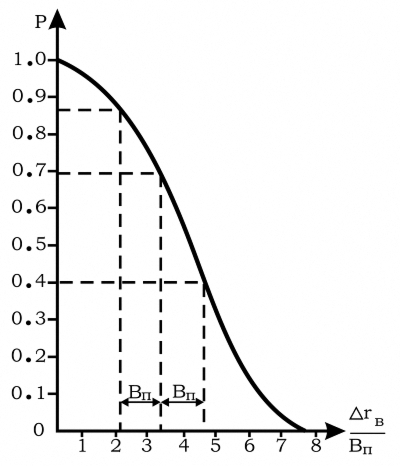{Рисунок 6}

Таким образом, если мы переместим точку прицеливания в сторону первой части, то вероятность его поражения будет в меньшей степени уменьшаться, чем уменьшится вероятное поражение второй части. Поэтому сумма вероятностей поражения обоих частей уменьшается. Из этого следует вывод, что для двух частей оптимальная точка прицеливания расположена в центре области возможного местоположения точки прицеливания.

При выборе точки прицеливания в случае необходимости относительная значимость частей цели может быть учтена путем присвоения более важной частью более высокого уровня P_{i тр}. Если найдены коэффициенты важности частей мишени, то для определения P_{i тр} можно использовать следующую формулу

где a_i — коэффициент важности части цели;

P_{i тр} — вероятное поражение части, определенное без учета его важности.

Рассматриваемый нами случай — это когда первоначальная вероятность поражения части меньше 0,5. На практике этот случай действительно имеет значение, поскольку установленная уверенность в поражении цели должна быть достаточно высокой.

Если цель состоит из более чем двух частей, то, как правило, перемещение точки прицеливания в сторону одной из частей увеличит расстояние между точкой прицеливания и остальными частями, что приведет к уменьшению суммы вероятностей поражения частей.

В зависимости от фактического расположения частей цели, данное правило в некоторых случаях может быть нарушено. Это происходит в случае, когда части цели располагаются на одной линии в размерах радиусов их зон поражения (рис. 7). Однако на практике такие цели встречаются очень редко. Кроме того, отклонение местоположений точек прицеливания от оптимального в этих условиях, как показывают расчеты, приводит к очень небольшому уменьшению значения математической вероятности поражения части цели.

Исходя из вышесказанного, можно сделать общий вывод: ПОСЛЕ ОПРЕДЕЛЕНИЯ ОБЛАСТИ ВОЗМОЖНЫХ ПОЗИЦИЙ ТОЧЕК ПРИЦЕЛИВАНИЯ, ТОЧКА ПРИЦЕЛИВАНИЯ ДОЛЖНА ОПРЕДЕЛЯТЬСЯ КАК ЦЕНТР ЭТОЙ ОБЛАСТИ; В СЛУЧАЕ, КОГДА ОБЛАСТЬ ВОЗМОЖНОГО РАСПОЛОЖЕНИЯ ТОЧЕК ПРИЦЕЛИВАНИЯ СОСТОИТ ИЗ ОТДЕЛЬНЫХ УЧАСТКОВ, ТОЧКИ ПРИЦЕЛИВАНИЯ ДОЛЖНЫ ОПРЕДЕЛЯТЬСЯ КАК ЦЕНТРЫ ЭТИХ УЧАСТКОВ.

В границы цели могут быть включены особо прочные [especially durable] части, для которых с данной величиной боевого заряда условие Pi≥P_{i тр} не выполняется. В этом случае мы применяем r_i = 0 и обозначаем особо прочная часть как точку прицеливания, если он находится в границах области возможных точек прицеливания остальных частей, иначе мы назначаем вторую точку цели (и увеличиваем расход ракет), если эта часть находится за границей области возможного расположения точек прицеливания для остальных частей. Эта вторая точка прицеливания, по сути, будет особо прочной частью.

{Рисунок 7}

При наличии нескольких таких частей расходы ракет определяется в соответствии с количеством частей; а точки прицеливания выбираются в центрах частей.

Вернемся к вопросу об определении необходимой вероятности поражения отдельных частей P_{i тр}.

При назначении огневой задачи может быть задано либо математическое ожидание поражения части цели M_тр, либо вероятность поражения всей цели P_тр .

Если задано математическое ожидание поражения части цели, то можно рассматривать ее как среднюю вероятность поражения отдельных частей. Затем:

Если задана вероятность поражения всей цели, то при определении требуемой вероятности поражения ее частей необходимо исходить из характера цели. В этом случае целесообразно разделить все цели на три группы:

1-я группа — цели, для поражения которых необходимо поражить все части;

2-я группа — цели, поражаемые поражением нескольких частей, различных в каждом отдельном случае;

3-я группа — цели, которые поражаются поражением даже одной части.

For targets of the first group, recognizing that the connection between the instances of destruction of separate elements in the employment of powerful charges is extremely close, the probability of destroying a separate element can almost be considered equal to the probability of destruction of the whole target. Then the required probability of destruction of a separate element is determined by the formula:

Для целей первой группы, принимая связь между экземплярами поражения отдельных частей при применении мощных зарядов чрезвычайно близкой, вероятность поражения отдельной части можно почти считать равной вероятности поражения всей цели. Тогда требуемая вероятность поражения отдельной части определяется по формуле:

For targets of the second and third groups it is necessary to establish the connection between the probability of destruction of the target and the mathematical expectancy of destruction of a portion of the target. It is easy to establish this connection, knowing the law of target destruction. The subsequent established mathematical expectancy is considered the median probability of destruction of separate elements and the required probability of destruction of an element is determined by equation (5).

Для целей второй и третьей групп необходимо установить связь между вероятностью поражения цели и математическим ожиданием поражения части цели. Легко установить эту связь, зная закон поражения цели. Следующее установленное математическое ожидание считается средней вероятностью поражения отдельных частей, а требуемая вероятность поражения части определяется уравнением (5).

The most complicated question is establishment of the law of target destruction. In the works of Colonel A.A. Chervonyy are presented and established possible hypotheses of types of laws of destruction of large targets, which permit us to reach a solution of the tasks which interest us.

Самым сложным вопросом является установление закона поражения цели. В работах полковника А.А. Червоного¹ представлены и устанавливаются возможные гипотезы о типах законов поражения крупных объектов, которые позволяют нам решать интересующие нас задачи.

For targets of the second group the most basic is the normal law of target destruction

Для целей второй группы самым основным является нормальный закон поражения цели

P = F_γ (10M - 5) ,      (7)

где F_γ — табличная функция F (x);

M — математическое ожидание поражения части цели.

Зная P_tr из таблицы функций F (x), мы можем найти M_tr и после с помощью уравнения (5) — P_{i tr}.

Основываясь на формуле (7) была составлена таблица для значений требуемой вероятности поражения части цели P_{i тр}, в зависимости от заданной вероятности поражения всей цели.

Эта таблица приведена ниже.

Значение P_{i тр} для целей второй группы

Таблица 1

For targets of the third group, the most expedient is acceptance of the hypotheses of the normal kind of function for assessment of the destroyed portion of the target:

Для целей третьей группы наиболее целесообразным является принятие гипотез нормального вида функции для оценки пораженной части цели:

где ξ — пораженная часть цели;

M — математическое ожидание поражения части цели;

Eξ - the median deflection of the destroyed portion of the target.

Eξ — среднее отклонение пораженной части цели.

For finding the unknowns M and Eξ it is necessary to equate the function (8) at two points, at which its vallie is known. As the first point we can take ξ i=1, where the function (8) for physical considerations is practically equal to 1. Accepting F (ξ ≤ 1) = 0.9996, we get,

Для нахождения неизвестных M и Eξ необходимо приравнять функцию (8) в двух точках, в которых известно ее значение. В качестве первой точки мы можем взять ξ _i = 1, где функция (8) для физических соображений практически равна 1. Принимая F (ξ ≤ 1) = 0,9996, получаем,

Eξ = 0.2 — 0.2 M.      (9)

As a second point we take the point ξ2 = 1/n, where n — is the number of elements comprising the target. If the target is destroyed by putting just one element out of action, then, evidently, the minimal destroyed portion of the target, with the assigned probability P_tr, is equal to 1/n . Then (

В качестве второй точки возьмем точку ξ2 = 1/n, где n — число частей, составляющих цель. Если цель поражена, даже если только одна часть поражена, то, очевидно, минимальная пораженная часть цели с назначенной вероятностью P_тр, равна 1/n. Далее,

F ( ξ ≤ 1/n) = 1 — P_тр.       (10)

Proceeding from P_tr according to formula (10) we determine the value ([missing]/n), then from the table for calculating the probability , we determine the value of the argument ((1/n — M) / Eξ) and taking into account equation (9), we find M. After which we equate it to P_{i tr}.

Исходя из P_тр согласно формуле (10), мы определяем значение ([отсутствует] / n), затем из таблицы для вычисления вероятности мы определяем значение аргумента ((1/n - M) / Eξ) и принимаем (9), найдем М. После этого мы приравняем его к P_{i тр}.

Ниже приведена таблица значений требуемой вероятности поражения частей в зависимости от заданной вероятности поражения цели и количества частей цели, рассчитанной по формулам (9) и (10).

Значения P_{i тр} для целей третьей группы

Исходя из вышеизложенного решения рассматриваемой задачи могут быть сформулированы следующие законы для выбора точек прицеливания:

1. На основе анализа цели определяется группа, к которой цель принадлежит.

2. Исходя из условий планируемой задачи, требуемая вероятность поражения частей цели определяется по формулам (5), (6) или согласно таблицам 1, 2 (в зависимости от характера цели) ,

3. Определяем величину Вп.

4. Определяем радиус зоны поражения для каждой части цели R_{a i}.

6. По известным R_{в i} и P_{i тр} согласно графику (рис. 4) определяем r_{в i} для каждой части цели.

7. Вычисляем r_i.

8. На плане цели, от центра каждой части, нарисуем окружности соответствующих радиусов r_i.

9. В области перекрытия всех кругов находим свой центр и принимаем его в качестве точку прицеливания.

10. Если область состоит из отдельных участков, то указываем количество ракет по количеству участков и выбираем центры участков в качестве точек прицеливания. Центр области определяется визуально.

Следует отметить, что во многих случаях целесообразно создавать графический макет не для всех частей (объектов) цели, а только для основных и важных. Это значительно уменьшает объем работы.

Предлагаемый графический метод выбора точек прицеливания для запуска баллистических ракет против разнородных целей является простым и в то же время обеспечивает достаточную точность на практике.

В заключение рассмотрим предложенный метод на конкретном примере.

Example. Target - Brise-Norton Air Base. The schematic plan of the base is presented below, in Figure 8. The assigned probability of destruction of the target P_tr =0.9 with a trotyl equivalent of 8 = 150 kilotons and a characteristic of dispersion of Vd = 1.4 km; Vb = 1 km.

Пример. Цель - авиабаза Брайз-Нортон². Схематический план базы представлен ниже на рисунке 8. Установленная вероятность поражения цели P_тр = 0,9 зарядом с тротиловым эквивалентом 8 [?, так в тексте] = 150 килотонн и характеристикой дисперсии Вд = 1,4 км; Вб = 1 км.

Выберите точку прицеливания.

Решение.

1. Определим уязвимые части цели и соответствующие им радиусы поражения:

— места стоянок самолетов 1, 2, 3; R_a1 = R_a2 = R_a3 = 4.3 км;

— диспетчерский пункт управления 4; R_a4 = 3.6 км

— жилые помещения 5; R_a5 = 3.6 км.

2. Определим Вп.

3. Мы определяем радиусы зон поражения в единицах Вп.

R_в1 = R_в2 = R_в3 = 3.5; R_в4 = R_в5 = 3

4. Applying the law of target destruction normally (a target of the second group), in Table 1 we determine the P_{i tr}, using the graph in Figure 4 - we get the r_vi and calculate these values in kilometers.

4. Обычно применяя закон поражения цели (цель второй группы), в таблице 1 мы определяем P_{i тр}, используя график на рисунке 4 - получаем r_{в i} и вычисляем эти значения в километрах.

r_в1 = r_в2 = r_в3 = 2.4; r_в4 = r_в5 =1.7;

r₁ = r₂ = r₃ = 2.9 км; r₄ = r₅ = 2 км.

5. На плане цели из центра каждой части мы нарисуем круги соответствующих радиусов и получим область возможного расположения точек прицеливания. На рисунке 8 эта область затенена внутри. [Качество документа не позволяет распознать "затенение", пожтому область показана красными границами, автор сайта]

6. Центр данной области выбран точкой прицеливания Тс (рисунок 8).

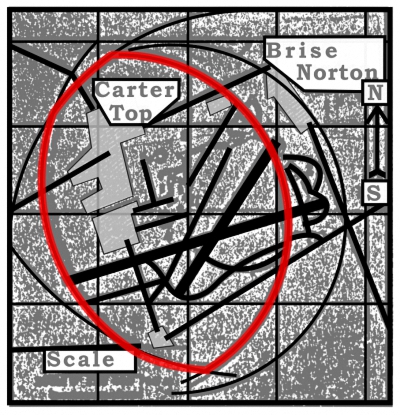{Рисунок 8}

В этом примере такие части [цели], как взлетно-опосадочная полоса, не были включены в цель. Эти части особенно прочны, и их поражение требует расходования зарядов большой мощности. Если в качестве уязвимых частей в данном примере мы включим взлетно-опосадочную полосу, то для нее r_i = 0; и точка прицеливания должна быть расположена на взлетно-посадочной полосе. Понятно, что это будет стык взлетно-посадочной полосы, которая не выходит за пределы области возможных мест назначения точек для отдельных частей.

Примечания автора сайта

¹ Полковник А.А. Червоный — В марте 1953 года в Военной артиллерийской инженерной академии имени Ф. Э. Дзержинского. на кафедре «Теории полета и аэродинамики управляемых реактивных снарядов» была создана группа стрельбы ракетами дальнего действия, которую возглавил А.А. Червоный. В связи с этим кафедра стала именоваться кафедрой «Теории полета, аэродинамики и стрельбы управляемыми реактивными снарядами» (сейчас - Кафедра «Теории полета и подготовки данных»).

В открытой печати известна книга — Червоный А.А., Шварц В.А., Козловцев А.П., Чобанян В.А. (Под ред. проф. А.А. Червоного) «Вероятностные методы оценки эффективности вооружения» (М.: Воениздат, 1979.) , посвященная близкой теме.

² Brise-Norton Air Base — Вполне реальная американская авиабаза.

Авиабаза Брайз-Нортон. Фото 1943 года