|
Ракета под влиянием тяжести. Вертикальное поднятие
27. Мы определили скорость приобретаемую ракетой в пустоте и при отсутствии силы тяготения, в зависимости от массы ракеты, массы взрывчатых веществ и энергии их химического соединения.
Разберем теперь влияние постоянной силы тяжести на вертикальное движение снаряда.
Мы видим, что без влияния тяжести приобретаются ракетой огромные скорости и утилизируется значительное количество энергии взрыва. Это будет справедливо и для среды тяжести, если только взрыв будет мгновенный. Ho такой взрыв для нас не годится, потому что при этом получится убийственный толчек, которого не вынесет ни снаряд, ни вещи и люди, заключенные в нем. Нам, очевидно, нужно медленное, взрывание; при медленном же взрывании полезный эффект уменьшается и даже может обратиться в нуль.
Действительно, пусть взрывание будет настолько слабо, что ускорение ракеты, происходящее от него, будет равно ускорению (g) земли. Тогда снаряд во все время взрывания, будет стоять в воздухе неподвижно без опоры.
Конечно он не приобретает при этом никакой скорости и утилизация взрывчатых веществ, не смотря на их количество, будет равняться нулю. Итак, крайне валено исследовать аналитически влияние на снаряд тяготения.
Когда ракета двигается в среде, свободной от силы тяжести, то время (t), в течении которого взрывается весь запас взрывчатого вещества, равно:
28. 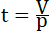 , где (V) есть скорость снаряда по окончании взрыва, а (p) постоянное ускорение, сообщаемое ракете взрывчатыми материалами в 1 секунду времени. , где (V) есть скорость снаряда по окончании взрыва, а (p) постоянное ускорение, сообщаемое ракете взрывчатыми материалами в 1 секунду времени.
Сила взрывания, т.. е. количество веществ, расходуемых при взрыве в единицу времени, в этом простейшем случае равномерно ускоряющегося движения снаряда, непостоянна, но непрерывно ослабляется – пропорционально уменьшению массы снаряда с остатком невзорванных материалов.
29. Зная (р), или ускорение в среде без тяжести, можем выразить и величину кажущейся (временной) тяжести внутри ракеты в течение ея ускоряющегося движения, пли в течение времени взрывания.
Приняв силу тяжести у поверхности земли за единицу, найдем величину временной тяжести в снаряде равной 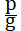 , где (g) есть земное ускорение; формула этз показывает, во сколько раз давление на подставки всех вещей, помещенных в ракете, больше давления тех же вещей, лежащих на столе в нашей комнате при обыкновенных условиях. Весьма важно знать величину относительной тяжести в снаряде, потому что она обусловливает целость или излом аппаратов и здоровье людей, пустившихся в путь для изучения неизвестных пространств п свойственных им явлений. , где (g) есть земное ускорение; формула этз показывает, во сколько раз давление на подставки всех вещей, помещенных в ракете, больше давления тех же вещей, лежащих на столе в нашей комнате при обыкновенных условиях. Весьма важно знать величину относительной тяжести в снаряде, потому что она обусловливает целость или излом аппаратов и здоровье людей, пустившихся в путь для изучения неизвестных пространств п свойственных им явлений.
30. При влиянии постоянной или переменной тяжести, любой силы, время, в течение которого расходуется один и тотже запас взрывчатого материала, будет тот-же, как и без влияния тяготения; оно выразится известною нам формулою (см. 28) или следующею:
31... 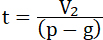 , где , где
(V2) есть скорость ракеты но окончании взрывания в среде тяжести с постоянным ускорением (g). Тут, конечно, предполагается, что (р) и (g) параллельны и противоположны (см. заглавие главы); (р–g) выражает видимое ускорение снаряда (относительно земли), являющееся результатом двух противоположных сил: силы взрыва и силы тяжести.
32. Действие последней на снаряд нисколько ни влияет на относительную в нем тяжесть и она выражается без всякого изменения формулой 29... 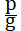 Напр., если р = 0, т. е. если взрывания нет, то нет и временной тяжести, потому что Напр., если р = 0, т. е. если взрывания нет, то нет и временной тяжести, потому что 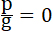 . Это значит, что если взрывание прекратится и снаряд двигается в ту или другую сторону только под влиянием своей скорости и силы тяготения солнца, земли и других звезд и планет, то находящийся в снаряде наблюдатель ни сам не будет иметь, повидимому, ни малейшего веса, – ни обнаружит его, при помощи самых чувствительных пружинных весов, ни в одной из вещей, находящихся при нем или в ракете. Падая или поднимаясь в ней под влиянием инерции даже у самой поверхности земли, наблюдатель не будет испытывать ни малейшей тяжести, пока, разумеется, снаряд не встречает никаких препятствий, – в виде, напр., сопротивления атмосферы, воды или твердого грунта. . Это значит, что если взрывание прекратится и снаряд двигается в ту или другую сторону только под влиянием своей скорости и силы тяготения солнца, земли и других звезд и планет, то находящийся в снаряде наблюдатель ни сам не будет иметь, повидимому, ни малейшего веса, – ни обнаружит его, при помощи самых чувствительных пружинных весов, ни в одной из вещей, находящихся при нем или в ракете. Падая или поднимаясь в ней под влиянием инерции даже у самой поверхности земли, наблюдатель не будет испытывать ни малейшей тяжести, пока, разумеется, снаряд не встречает никаких препятствий, – в виде, напр., сопротивления атмосферы, воды или твердого грунта.
33. Если p = g, т. е. если давление взрывающихся газов равно тяжести снаряда (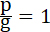 ), то относительная тяжесть будет равняться
земной. При начальной неподвижности, снаряд в этом случае и остается неподвижным во все время действия взрыва; если же до него снаряд имел какую нибудь скорость (вверх, вбок, вниз), то эта скорость так и останется без всякого изменения, пока не израсходуется весь взрывчатый материал: тут тело, т. е ракета уравновешена и двигается как бы по энерции в среде, свободной от тяжести. ), то относительная тяжесть будет равняться
земной. При начальной неподвижности, снаряд в этом случае и остается неподвижным во все время действия взрыва; если же до него снаряд имел какую нибудь скорость (вверх, вбок, вниз), то эта скорость так и останется без всякого изменения, пока не израсходуется весь взрывчатый материал: тут тело, т. е ракета уравновешена и двигается как бы по энерции в среде, свободной от тяжести.
Нa основании формул 28 и 31 получим:
34... 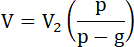
Отсюда, зная какую скорость (V2) должен иметь но окончании взрыва снаряд, мы вычислим (V), по которой, с помощью формулы 16 определим и потребное количество (M2) взрывчатых веществ.
Из уравнений 16 и 31 получим:
35. 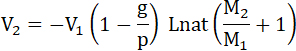
36. Из этой формулы, также как из предыдущей, следует, что скорость, приобретаемая ракетой, меньше при влияния тяготения, чем без него (16). Оно (V2) может быть даже равна нулю, не смотря на обилие взрывчатого запаса, если 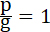 , т. е. еслп ускорение, сообщаемое снаряду взрывчатым материалом, равно ускорению земной тяжести, или – давление газов равно и прямо противоположно действию тяготения. (См. форм. 34 и 35). , т. е. еслп ускорение, сообщаемое снаряду взрывчатым материалом, равно ускорению земной тяжести, или – давление газов равно и прямо противоположно действию тяготения. (См. форм. 34 и 35).
В этом случае ракета стоит несколько минут неподвижно, нисколько не поднимаясь; когда же запас истощен, она падает, как камень.
37. Чем больше (р) по отношению (g), тем большую скорость (V2) приобретает снаряд при данном количестве (М2) взрывчатых веществ (форм. 35).
Поэтому, желая подняться выше, надо сделать (р) как можно больше, т. е. производить взрыв как можно деятельнее. Однако, при этом, во-первых, требуется более крепкий и массивный снаряд, во вторых, – более крепкие предметы и аппараты в снаряде, потому что (по 32) относительная тяжесть в нем будет весьма велика и в особенности опасна для живого наблюдателя, если таковой отправляется в ракете.
Во всяком случае, на основании формулы 35-й, в пределе,
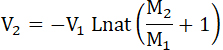
т. е., если (р) безконечно велико, или взрыв моментален, то скорость (V2) ракеты в среде тяжести та-же, что и в среде без тяжести.
Согласно формуле 30 время взрывания не зависит от силы тяготения, а лишь исключительно от количества (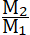 ) взрывчатого мате
риала и быстроты их взрывания (р). ) взрывчатого мате
риала и быстроты их взрывания (р).
39. Любопытно определить эту величину. Положим в форм. 28 V = 11.100 метров (см. таблицу 22); a p = g = 9,8 метра; тогда t = 1.133 секунды.
Значит в среде, свободной от тяжести, ракета пролетела бы равномерно ускоряющимся движением менее 19 минут – и это при ушестеренном количестве взрывчатых веществ сравнительно с массою снаряда (см. табл. 22).
При взрывании-же у поверхности нашей планеты, он простоял бы неподвижно в течении тех же 19 минут.
40. Если 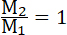 то, по табл. V = 3.920 метров; следовательно,
t = 400 секундам, или 6 2/3 минуты. то, по табл. V = 3.920 метров; следовательно,
t = 400 секундам, или 6 2/3 минуты.
При 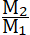 = 0,1, V = 543 метра, a t = 55,4 секунды, т. е. менее минуты. В последнем случае, у поверхности земли, снаряд простоял бы неподвижно 551/2 секунд. = 0,1, V = 543 метра, a t = 55,4 секунды, т. е. менее минуты. В последнем случае, у поверхности земли, снаряд простоял бы неподвижно 551/2 секунд.
Отсюда мы видим, что взрывание у поверхности планеты, или вообще в среде, несвободной от силы тяжести, может быть совершенно безрезультатным, если происходит, хотя и долгое время, но с недостаточною силою: действительно, снаряд остается на месте п не получает никакой поступательной скорости, если не приобрел ее раньше; в противном случае, он может совершить некоторое перемещение с равномерною скоростью. Если это перемещение совершается вверх, то снаряд сделает некоторую работу. В случае первоначальной горизонтальной скорости и перемещение будет горизонтально; работы тут не будет, но тогда снаряд может служить для таких-же целей, как локомотив, пароход, или управляемый аэростат. Служить для этих целей перемещения снаряд может только в течении нескольких минут, пока совершается взрывание, но и в такое небольшее время он может пройти значительное пространство, в особенности если будет двигаться над атмосферой. Впрочем, практическое значение ракеты для летания в воздухе мы отрицаем.
Время стояния прибора в среде тяготения обратно пропорционально (g), т. е. силе этого тяготения.
Так на луне прибор простоял бы неподвижно без опоры (при 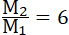 ) в течение 2 часов. ) в течение 2 часов.
41. Положим в формуле 35, для среды с тяжестью:
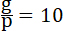 ; ; 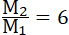 тогда вычислим V2 = – 9990 метров. Относительная тяжесть, по предыдущему, будет равна 10, т. е. человек в 70 килограммов весом, во все время взрывания (около 2 минут), будет испытывать тяжесть в 10 раз большую, чем на земле и будет весить на пружинных весах 700 килограммов (пудов 40). Такую тяжесть путешественник может перенести без вреда только при соблюдении особых предосторожностей: при погружении в особую жидкость, при особенных условиях. тогда вычислим V2 = – 9990 метров. Относительная тяжесть, по предыдущему, будет равна 10, т. е. человек в 70 килограммов весом, во все время взрывания (около 2 минут), будет испытывать тяжесть в 10 раз большую, чем на земле и будет весить на пружинных весах 700 килограммов (пудов 40). Такую тяжесть путешественник может перенести без вреда только при соблюдении особых предосторожностей: при погружении в особую жидкость, при особенных условиях.
На основании формулы 28, вычислим и время взрывания, или время этой усиленной тяжести; получим 113 секунд, т. е. менее двух минут. Это очень немного и кажется с первого раза поразительным, как может снаряд в течение такого ничтожного промежутка времени приобрести скорость, чуть недостаточную для удаления от земли и движения вокруг солнца подобно новой планете.
Мы нашли V2 = 9990 метров, т, е. такую скорость, которая лишь немного менее скорости (V), приобретаемой в среде, свободной от силы тяготения, при тех же условиях взрыва (см. табл. 22). Ho так как снаряд во время взрывания еще и поднимается на некоторую высоту, то приходит даже в голову, что общая работа взрывчатых веществ совсем не уменьшалась, сравнительно с работою их в среде без тяжести.
44. Вопрос этот мы сейчас разберем.
Ускорение снаряда в среде тяжести выразится р1 = p-g
На расстоянии от поверхности земли, не превышающем нескольких сотен верст, мы (g) примем постоянным, что не повлечет за собой большой погрешности; да и погрешность то будет в благоприятную сторону, т. е. истинныя числа будут благоприятнее для полета, чем вычисленные нами.
Высота (h) поднятие снаряда, во время (t) действия взрыва, будет.
45... 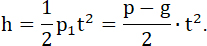
Выключая отсюда (t), по уравнению 31, получим:
46... 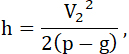
где (V2) есть скорость снаряда в среде тяжести, по истощении всего, взрывчатого запаса.
Теперь получим из 34 и 46 выключая (V2):
47... 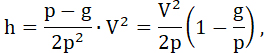
где (V) есть скорость, приобретаемая ракетой в среде, свободной от тяготения. Полезная работа взрывчатых веществ в такой среде выразится:
48... 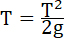
Работа же (T1) в среде тяжести выразится, в зависимости от высоты поднятия снаряда и его скорости по окончании взрыва:
49... 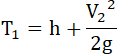
Отношение этой работы к предыдущей, идеальной, равно:
50... 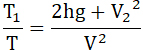
Исключив отсюда (h) и (V), посредством 46 и 34, найдем:
51... 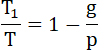
т. е. работа в среде тяготения, получаемая от определенного количества взрывчатых веществ (M2), менее, чем в среде свободной от
него: разница эта (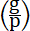 ) тем меньше, чем быстрее вырываются газы, или
чем более (р). Напр., в случае (41), потеря составляет только 1/10, а утилизация (51) равна 0,9. Когда p=g, или когда снаряд стоит в воздухе, не имея даже постоянной скорости, потеря будет полная (1), а утилизация равна нулю. Такова же будет утилизация, если снаряд имеет постоянную горизонтальную скорость. ) тем меньше, чем быстрее вырываются газы, или
чем более (р). Напр., в случае (41), потеря составляет только 1/10, а утилизация (51) равна 0,9. Когда p=g, или когда снаряд стоит в воздухе, не имея даже постоянной скорости, потеря будет полная (1), а утилизация равна нулю. Такова же будет утилизация, если снаряд имеет постоянную горизонтальную скорость.
52. В парагр. 41 мы вычислили V2 = 9990 метров. Применим формулу 46 к случаю 41, найдем: h=565 километров; значит, в течении взрыва, снаряд зайдет далеко за пределы атмосферы и приобретет еще поступательную скорость в 9990 метров.
Заметим, что скорость эта на 1.110 метров меньше, чем в среде, свободной от силы тяготения. Эта разность составляет как раз 1/10 скорости в среде без тяжести (см. табл. 22).
Отсюда видно, что потеря в скорости подчиняется тому же закону, как и потеря работы (см. 18), что, впрочем, строго следует и из формулы 10, преобразуя которую получим:
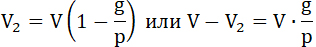
Найдем из 51:
56... 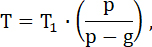
где (T1) есть работа, получаемая снарядом от взрывчатых веществ в среде тяготения, сила которого равна (g).
Чтобы снаряд мог совершить все необходимые работы, поднимаясь в высоту, преодолевая сопротивление атмосферы и приобретая желаемую скорость, – необходимо, чтобы сумма всех этих работ равнялась (T1).
Когда определим все эти работы, то с помощью формулы 56, вычислим Т. Зная же (T), вычислим и (V), т.-е. скорость в среде без тяжести по формуле:
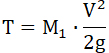
Зная теперь (V), можем рассчитать и потребную массу (M2) взрывчатых веществ по формуле 16.
Таким путем, с помощью предыдущего, найдем:
57 ... 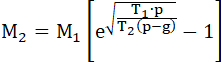
Вычисляя, мы (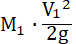 ) заменили для краткости через (T2). ) заменили для краткости через (T2).
Итак, зная массу снаряда (M1) со всем содержимым, кроме взрывчатого материала (M2), механическую работу (Т2) взрывчатых веществ при массе их, равной массе снаряда (Μ1), работу (T1), которую должен совершить снаряд при своем вертикальном поднятии, силу взрывания (p) и силу тяготения (g), – можем узнать и количество взрывчатых веществ (M2), необходимое для поднятия массы (M1) снаряда.
Отношение 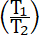 в формуле не изменится, если его сократить на
(Μ1). Так, что под (T1) и (T2) можно подразумевать механическую работу (T1), совершаемую единицею массы снаряда и механическую работу (T2), единицы взрывчатых веществ. в формуле не изменится, если его сократить на
(Μ1). Так, что под (T1) и (T2) можно подразумевать механическую работу (T1), совершаемую единицею массы снаряда и механическую работу (T2), единицы взрывчатых веществ.
Под (g) нужно, вообще, подразумевать постоянное сопротивление, равное сумме сил тяжести и сопротивление среды. Ho сила тяготения постепенно убывает с удалением от центра земли, вследствие чего утилизируется большее количество механической работы взрывчатых веществ. С другой стороны, сопротивление атмосферы, будучи, как увидим, сравнительно с тяжестью снаряда, весьма незначительным. – уменьшает утилизацию энергии взрывчатых веществ.
По некотором размышлении увидим, что последняя убыль, продолжаясь недолгое время пролета через воздух, с избытком вознаграждается прибылью от уменьшения притяжения на расстояниях значительных (500 килом.), где кончается действие взрывчатых веществ.
Итак, формулу 20 можем смело применять к вертикальному поднятию снаряда, несмотря на осложнение от изменения тяжести и сопротивления атмосферы (g = 9,8 метров).
* * *
|