|
Ракета в среде, свободной от тяжести и атмосферы
6. Сначала рассмотрим действие в среде, свободной от тяжести и окружающей материи, т. е. атмосферы. Относительно последней мы беремся только разобрать ее сопротивление движению снаряда, но не движению вырывающихся стремительно паров. Влияние атмосферы на взрыв не совсем ясно: с одной стороны оно благоприятно, потому что вырывающиеся вещества имеют в окружающей материальной среде некоторую опору, которую они, при своем движении, увлекают и таким образом способствуют увеличению скорости ракеты; но с другой стороны, та же атмосфера, своей плотностью и упругостью мешает расширению газов далее известного предела, от чего взрывчатые вещества не приобретают той скорости, которую они могли бы приобрести, взрываясь в пустоте. Это последнее влияние неблагоприятно, потому что приращение скорости ракеты пропорционально скорости отбрасываемых продуктов взрыва.
7. Мaccy снаряда со всем содержимым, кроме запаса взрывчатых веществ, обозначим через M1; полную массу последних через M2; наконец, переменную массу взрывчатых веществ, оставшихся невзорванными в снаряде в данный момент – через M.
Таким образом, полная масса ракеты, при начале взрыва будет равна (M1+M2); спустя же некоторое время, она выразится переменной величиною (M1+M); наконец, по окончании взрывания, – постоянной M1.
Чтобы ракета получила наибольшую скорость, необходимо чтобы отбрасывание продуктов взрыва совершалось в одном направлении относительно звезд. А для этого нужно, чтобы ракета не вращалась; а чтобы она не вращалась, надо чтобы равнодействующая взрывающих сил, проходящая через центр их давления, проходила в то же время и через центр инерции всей совокупности летящих масс. Вопрос, как этого достигнуть на практике, мы уже слегка разобрали.
Итак, предполагая такое наивыгоднейшее отбрасывание газов в одном направлении, получим следующее дифференциальное уравнение, на основании закона о постоянстве количества движения:
8... 
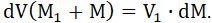
9. Здесь dM есть бесконечно-малый отбросок взрывчатого вещества, вырывающегося из пушечного раструба с постоянною относительно ракеты скоростью (V1).
10. Я хочу сказать, что относительная скорость (V1) вырывающихся элементов, при одинаковых условиях взрыва, одна и та же во все время взрывания, – на основании закона относительных движений; (dV) есть приращение скорости (V) движения ракеты вместе с оставшимися нетронутыми взрывчатыми материалами; приращение это (dV) совершается, благодаря отбрасыванию элемента (dM) со скоростью (V1). Определением последней мы займемся в своем месте.
11. Разделяя переменные величины в уравнении 8 и интегрируя, получим:
12... 
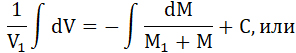
13... 
_________________
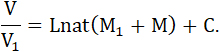
*) (Lnat) есть натуральный логарифм.
Тут C есть постоянное. Когда M=M2, т. е. до взрывания, V = 0; на этом основании найдем:
14...  *)
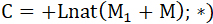стало быть
15... 
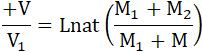
Наибольшая скорость снаряда получится, когда M = 0, т. е., когда весь запас (M2) взорван; тогда получим, полагая в предыдущем уравнении M = 0:
16... 
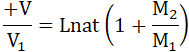
17. Отсюда мы видим, что скорость (V) снаряда возрастает неограниченно с возрастанием количества (M2) взрывчатых веществ. Значит, запасаясь разными количествами их, при разных путешествиях, мы получим самые разнообразные окончательные скорости. Из уравнения 16 также видно, что скорость ракеты, по израсходовании определенного запаса взрывчатого вещества, не зависит от быстроты или неравномерности взрывания, лишь бы частицы отбрасываемого материала двигались с одной и тою же скоростью (V1) относительно ядра.
Однако, с увеличением запаса (M2), скорость (V) ракеты возрастает все медленнее и медленнее, хотя и безгранично. Приблизительно, она возрастает, как логарифм от увеличения количества взрывчатых запасов (M2), (если M2 велико в сравнении с M1, т.-е. масса взрывчатых веществ в несколько раз больше массы снаряда).
18. Дальнейшие вычисления будут интересны, когда мы определим (V1), т.-е. относительную и окончательную скорость взорванного элемента. Так как газ или пар, при оставлении пушечного раструба, весьма разрежается и охлаждается (при достаточной длине трубы) – даже обращается в твердое состояние, – в пыль, которая мчптся с страшною быстротою, – то можно принять, что вся энергия горения, или химического соединения, при взрывании, обращается в движение продуктов горения, или в кинетическую энергию. В самом деле, представим себе определенное количество газа, расширяющегося в пустоте, без всяких приборов: он будет во все стороны расширяться и вследствие этого охлаждаться до тех пор, пока не превратится в капли жидкости, или в туман.
Туман этот обращается в кристаллики, но уже не от расширения, а от испарения и лучеиспускания в мировое пространство.
Расширяясь, газ выделит всю свою явную и отчасти скрытую энергию, которая превратится в конце концов в быстрое движение кристалликов, направленное во все стороны, так как газ расширялся свободно во все стороны. Если же его заставить расширяться в резервуаре с трубой, то труба направит движение газовых молекул по определенному направлению, чем мы и пользуемся для наших целей, т.-е. для движения ракеты.
Как будто энергия движения молекул превращается в кинетическое движение до тех пор, пока вещество сохраняет газообразное или парообразное состояние. Ho это не совсем так. Действительно, часть вещества может обратится в жидкое состояние; но при этом выделяется энергия (скрытая теплота парообразования), которая передается оставшейся парообразной части материи и замедлить на некоторое время переход ея в жидкое состояние.
Подобное явление мы видим в паровом цилиндре, когда пар работает собственным расширением, выход же из парового котла в цилиндр заперт. Тогда, при какой бы температуре не был пар, часть его обращается в туман, т.-е. жидкое состояние, другая же часть продолжает сохранять парообразное состояние и работать, заимствуя скрытую теплоту сгустившихся в жидкость паров.
Итак, энергия молекулярная будет превращаться в кинетическую, по крайней мере, до состояния жидкого. Когда вся масса обратится в капли, превращение в кинетическую энергию почти приостановится, потому что пары жидких и твердых тел, при низкой температуре, имеют черезчур незначительную упругость и использование их на практике затруднительно, так как потребует огромных труб.
И еще некоторая незначительная часть указанной нами энергии пропадет для нас, т.-е. не превратится в кинетическую энергию, благодаря еще и трению о трубу и лучеиспусканию теплоты нагретыми ея частями. Впрочем, труба может быть окружена кожухом, в котором циркулирует какой-нибудь жидкий металл; он передаст жар весьма нагретой части одного конца трубы другой ее части, охлажденной вследствие сильного разрежения паров. Таким образом, и эта потеря, от лучеиспускания и теплопроводности, может быть утилизирована или сделана очень незначительной. В виду кратковременности взрывания, продолжающегося в крайних случаях от 2 до 5 минут, потеря от лучеиспускания и без всяких приспособлений незначительна; циркуляция же металлической жидкости в кожухе, окружающем трубы, необходима для другой цели: для поддержания труб при одной и той же невысокой температуре, т.-е. для сохранения крепости трубы. Несмотря на это, возможно, что часть ея будет расплавлена, окислена и унесена вместе с газами и парами. Может быть, для избежания этого, внутреннюю часть трубы будут выкладывать каким-нибудь особенным огнеупорным материалом, углеродом, вольфрамом, или чем-нибудь иным. Хотя часть углерода при этом и сгорит, но крепость металлической пушки, мало нагретой, пострадать от этого не может.
Газообразный же продукт горения углерода – углекислота только усилит поднятие ракеты. Может быть употреблен будет род тигельного материала – какая-нибудь смесь веществ. Во всяком случае, не я решу этот вопрос, как и множество других, относящихся к нашим реактивным приборам.
Во многих случаях я принужден лишь гадать пли предполагать. Я нисколько не обманываюсь и отлично знаю, что не только не решаю вопроса во всей полноте, но что остается поработать над ним в 1000 раз больше, чем я работал. Моя цель возбудить к нему интерес, указав на великое значение его в будущем и на возможность его решения... Для уменьшения протяжения, занимаемого трубами при той же длине их, можно завивать их кольцами пли змеевиком, окруженным, для сохранения умеренной и равномерной температуры, хорошо проводящей тепло и быстро циркулирующей жидкостью. Это будет способствовать устойчивости ракеты, особенно, если обороты будут в двух взаимно перпендикулярных направлениях. Только центробежная сила газов несколько усилит давление в трубах.
В настоящее время обращение водорода и кислорода в жидкость не представляет особенных затруднений. Можно водород заменить жидкими или сгущенными в жидкость углеводородами, напр. ацетиленом, нефтью. Жидкости эти должны быть разделены перегородкой. Температура их весьма низкая; поэтому ими полезно окружать или кожухи с циркулирующим металлом, или непосредственно самые трубы.
Опыт покажет как сделать лучше. Некоторые металлы делаются крепче от охлаждения; вот такие то металлы и нужно употребить, напр, железо. He помню хорошо, но какие то опыты, над сопротивлением, кажется, железа, в жидком воздухе, указали, что вязкость его при этой низкой температуре увеличивается чуть ли не в десятки раз. За достоверность не ручаюсь, но опыты эти, в применении к нашему делу, заслуживают глубочайшего внимания. (Почему бы не охлаждать таким образом и обыкновенные пушки, прежде чем из них стрелять; ведь жидкий воздух теперь такая обыкновенная вещь).
Жидкий кислород и такой же водород, выкачиваемые из своих резервуаров, в известном отношении, в узкое начало трубы и соединяясь тут понемному, могут дать прекрасный взрывчатый материал. Получаемый при химическом соединении этих жидкостей водяной пар, при страшно высокой температуре, будет расширяться, подвигаясь к концу, или устью трубы до тех пор, пока не охладится до того, что обратится в жидкость, несущуюся в виде тончайшего тумана по направлению длины трубы, к ея выходу (раструбу).
19. Водород и кислород, в газообразном состоянии, соединяясь для образования одного килограмма воды, развивают 3825 калорий. Под словом «калория» мы тут подразумеваем количество теплоты, потребное для нагревания на 1 Цельсия одного килограмма воды.
Количество это (3825) у нас будет немного меньше, раз кислород и водород находится в жидком состоянии, а не в газообразном, к каковому относится данное нами число калорий. В самом деле, жидкости, во-первых, надо нагреть, во-вторых обратить в газообразное состояние, на что расходуется некоторая энергия. В виду незначительной величины этой энергии, сравнительно с энергией химической, мы оставим наше число без умаления (этот вопрос не совсем выяснен наукой, но мы водород и кислород берем только для примера).
Принимая механический эквивалент теплоты в 424 килограметра, найдем, что 3825 колорий соответствуют работе в 1.621.800 килограмметров; этого достаточно для поднятия продуктов взрыва, т. е. одного килограмма вещества, на высоту 1.622 километра от поверхности земного шара, предполагая силу тяжести, постоянной. Эта работа, превращенная в движение, соответствует работе одного килограмма массы, движущейся со скоростью 5.700 метров в 1 секунду. Я не знаю ни одной группы тел, которые, при своем химическом соединении, выделяли бы, на единицу массы полученного продукта, такое огромное количество энергии. Кроме того, некоторые другия вещества, соединяясь, необразуют летучих продуктов, что для нас совсем не годится. Так кремний, сгорая в кислороде (Si+O2 = SiO2), выделяет огромное количество тепла, именно 3654 калории на единицу массы полученного продукта (SiO2), но к сожалению образуются трудно-летучие тела.
Приняв жидкий кислород и водород за материал, наиболее пригодный для взрывания, я дал число для выражения их взаимной химической энергии, приходящейся на единицу массы полученного продукта (H2O), несколько большее истинного» так как вещества, соединяющиеся в ракете, должны находиться в жидком, а не в газообразном состоянии, и кроме того при очень низкой температуре.
Считаю нелишним тут утешить читателя, что не только на эту энергию (3825 кил.), но и на несравненно большую мы можем надеяться в будущем, когда может быть найдут возможным осуществить наши недовольно разработанные еще мысли. В самом деле, рассматривая количество энергии, получаемой от химических процессов разнообразных веществ, замечаем в общем, не без исключений, конечно, что количество энергии, приходящейся на единицу массы продуктов соединения, зависит от атомных весов, (в большинстве случаев) соединяющихся простых тел; чем меньше атомные веса тел, тем более выделяется при соединений их тепла. Так, при образовании сернистого газа (SO2), образуется только 1250 калорий, а при образовании окиси меди (CuO) – только 546 калорий; между тем как уголь, при образовании углекислоты (CO2), выделяет на единицу ее массы 2204 калории. Водород с кислородом, как мы видим, выделяют еще больше (3825). Для оценки этих данных, в применении к высказанной мною идее, напомню тут величину атомных весов приводимых элементов: водород = 1; кислород = 16; углерод = 12; сера = 33; кремний = 28; медь = 63.
Конечно, можно привести и много исключений из этого правила, но в общем оно справедливо. Действительно, если мы вообразим ряд точек, абсциссы которых выражают сумму (или произведение) атомных весов соединяющихся простых тел, а ординаты соответствующую энергию химического соединения, то проведя через точки (по возможности ближе к ним) плавную кривую, увидим непрерывное уменьшение ординат но мере увеличения абсцисс, чем и доказывается наш взгляд.
Поэтому, если когда-нибудь, так называемые, простые тела окажутся сложными и их разложат на новые элементы, то атомные веса последних должны быть меньше известных нам простых тел. Ново-открытые элементы по предыдущему, должны выделять при своем соединении несравненно большее количество энергии, чем тела, считаемые теперь условно простыми и имеющие сравнительно большой атомный вес.
Самое существование эфира с его почти безпредельною упругостью и громадною скоростью его атомов, указывает на беспредельно малый атомный вес этих атомов и беспредельную энергию в случае их химического соединения.
20. Как бы то ни было, но пока для V1 (см. 15 и 19) мы не можем принять более 5700 метров в 1 секунду. Ho со временем, кто знает, может быть это число увеличится в несколько раз.
Принимая 5700 метров, можем по формуле 16 вычислить не только
отношение скоростей 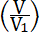 но и абсолютную величину окончательной
(наибольшей) скорости (V) снаряда, в зависимости от отношения .
21. Из формулы 16 видно, что масса ракеты со всеми пассажирами и всеми аппаратами (M1) может быть произвольно велика и скорость (V) снаряда от этого нисколько не потеряет, лишь бы запас взрывчатых веществ (M2) возростал пропорционально возростанию массы (M1) ракеты.
Итак, всевозможной величины снаряды, с любым числом путешественников, могут приобретать скорости желаемой величины. Впрочем, возростания скорости ракеты сопровождается, как мы видели, несравненна быстрейшим возрастанием массы (M2) взрывчатых веществ; Поэтому насколько легко и возможно увеличение массы поднимающегося в небесное пространство снаряда, настолько затруднительно увеличение его скорости.
22. Из уравнения 16 получим следующую таблицу:
 |
 |
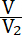Секундная
скорость (V)
в метрах. |
|
|
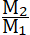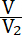Секундная
скорость (V)
в метрах. |
| 0,1 |
0,095 |
543 |
7 |
2,079 |
11,800 |
| 0,2 |
0,182 |
1,037 |
8 |
2,197 |
12,500 |
| 0,3 |
0,262 |
1,493 |
9 |
2,303 |
13,100 |
| 0,4 |
0,336 |
1,915 |
10 |
2,398 |
13,650 |
| 0,5 |
0,405 |
2,308 |
19 |
2,996 |
17,100 |
| 1 |
0,693 |
3,920 |
20 |
3,044 |
17,330 |
| 2 |
1,098 |
6,260 |
30 |
3,434 |
19,560 |
| 3 |
1,386 |
7,880 |
50 |
3,932 |
22,400 |
| 4 |
1,609 |
9,170 |
100 |
4,615 |
26,280 |
| 5 |
1,792 |
10,100 |
193 |
5,268 |
30,038 |
| 6 |
1,946 |
11,100 |
Бесконечно. |
Безконечно. |
23. Из нее усматриваем, что скорости, получаемые реактивным путем, далеко немалы. Так при массе взрывчатых веществ, в 193 раза перевышающей вес (M1) снаряда (ракеты), скорость его, по окончании взрывания и израсходования всего запаса (M2), равна скорости движения земли вокруг солнца. He думайте, что такая громадная масса взрывчатого материала требует для своего сохранения громадного количества крепкого материала для сосудов, содержащих взрывчатые элементы. Действительно, водород и кислород в жидком виде только тогда обнаруживают высокое давление, когда сосуды, содержащие их, заперты, т.-е. когда самые газы, влиянием окружающих сравнительно теплых тел, нагреются. У нас же эти сжиженные газы должны иметь свободный выход в трубу (помимо постоянного притока их туда в жидком виде), где они, соединяясь химически, взрывают.
Непрерывное и быстрое течение газов, соответствующее испарению жидкостей, охлаждает эти последние до того, что они, своими парами, не производят почти никакого давления на окружающие их стенки. Итак, для сохранения элементов взрыва, не требуется на сосуды большой массы вещества.
24. Когда запас взрывчатого вещества равен массе ракеты 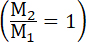 , то скорость последней чуть не вдвое более той, которая нужна, чтобы камню или пушечному ядру, пущенному, «селенитами» с поверхности нашей луны, удалиться от нее навсегда и сделаться спутником земли, второй луной.
Эта скорость (3920 метров в секунду) почти достаточна для вечного удаления тел, брошенных с поверхности Марса или Меркурия.
Если отношение
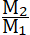масс будет 3, то уже получится, по израсходовании всего запаса, такая скорость снаряда, которой лишь немного не достает для того, чтобы он мог вращаться за пределами атмосферы, вокруг земли, подобно ее спутнику.
При отношении
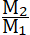равном С, скорость ракеты почти достаточна для удаления ее от земли и вечного вращения вокруг солнца в качестве самостоятельной планеты. При большом количестве взрывчатого запаса, возможно достижение пояса Астероидов и даже тяжелых планет.
25. Из таблицы видно, что и при небольшом запасе взрывчатых веществ, окончательная скорость снаряда еще достаточна для практических целей. Так при запасе, составляющем лишь 0,1 веса ракеты, скорость равна 543 метрам в секунду, что довольно для поднятия ракеты на 15 километров. Далее из таблицы мы видим, что при незначительном запасе, скорость, по окончании взрыва приблизительно, пропорциональна массе запаса (M2); следовательно, в этом случае, высота поднятия пропорциональна квадрату этой массы (M2) запаса. Так, при запасе, составляющем половину массы ракеты (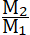) = 0,5
последняя залетит далеко за пределы атмосферы.
26. Интересно определить, какая часть полной работы взрывчатых веществ, т. е. их химической энергии, передается ракете.
Работа взрывчатых веществ выразится  ,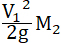
где (g) есть ускорение земной тяжести; механическая работа ракеты, имеющей скорость (V), выразится в тех же единицах:
 ,
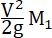или, На основаниях формулы 16:
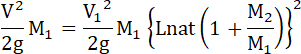
Разделив теперь работу ракеты на работу взрывчатого материала, получим:
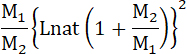
Пo этой формуле вычислим следующую таблицу утилизации ракетой энергии взрывчатых веществ.
Из Формулы и таблицы видно, что при очень малых количествах
взрывчатого материала утилизация его равна ,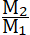
т. е. тем меньше,
чем относительное количество взрывчатых веществ меньше. *)
|
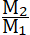Утили-
зация. |
|
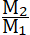Утили-
зация. |
| 0,1 |
0,090 |
7 |
0,62 |
| 0,2 |
0,165 |
8 |
0,60 |
| 0,3 |
0,223 |
9 |
0,59 |
| 0,4 |
0,282 |
10 |
0,58 |
| 0,5 |
0,328 |
19 |
0,47 |
| 1 |
0,480 |
20 |
0,46 |
| 2 |
0,600 |
30 |
0,39 |
| 3 |
0,64 |
50 |
0,31 |
| 4 |
0,65 |
100 |
0,21 |
| 5 |
0,64 |
193 |
0,144 |
| 6 |
0,63 |
Бесконечно. |
Нуль. |
Далее, с увеличением относительного количества взрывчатых веществ, утилизация возрастает и, приблизительно, при учетверенном их количестве (сравнительно с массой ракеты), достигает наибольшей величины (0,65).
___________________
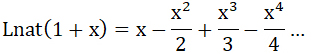*) Действительно  ... Следовательно, приблизительно,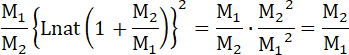 
Дальнейшее увеличение взрывчатых веществ, хотя и медленно, но непрерывно уменьшает их полезность, при бесконечно-большом их количестве, она нуль, также как и при бесконечно-малом. Из таблицы также видпм, что при изменении отношения (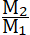) от 2 до 10, утилизация более половины; это значит, что в таком случае более половины потенциальной энергии взрывчатого материала передается в виде кинетической энергии ракете. Вообще от 1 до 20 она весьма велика и близка к 0,5.
* * *
|
