|
о) Закрытая пушка с реактивным снарядом.
Предположим, что внутри обыкновенной закрытой в казенной части пушки находится реактивный снаряд. Пусть сорт пороха, форма сопла и прочность стенок камеры сгорания снаряда таковы, что получается значительная разница давлений внутри камеры снаряда и внутри пушки; тогда извергающийся из сопла газ произведет реакцию, и его кинетическая анергия, благодаря ударам и вихрям, преобразуется в тепловую.
В некоторый момент t снаряд передвинется внутри канала на путь х и газ, находящийся внутри канала, будет в таком же состоянии, как и в обыкновенной пушке одинаковой силы, когда полностью сгорит ее заряд:
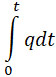
и произведет работу:
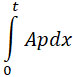
Здесь p – давление в канале пушки.
Этих положений было бы достаточно для составления дифференциальных уравнений, необходимых для решения задачи. Однако, аналитическое интегрирование их весьма сложно, так как нет экспериментальных данных о распределении давлений внутри канала во время пути снаряда.
В виду отсутствия этих данных, мы ограничимся в настоящем исследовании приближенной теорией, основанной на результатах, полученных при изучении полета свободного снаряда.
Диаграмма px нашей пушки будет аналогична таковой же для обыкновенной пушки, разве только сместится ордината, соответствующая максимальному давлению. Для первого приближения предположим, что среднее давление в нашем случае эквивалентно таковому же в обычной пушке при равных весах заряда и снаряда.
Разность давлений внутри камеры снаряда и внутри канала пушки (каковая должна быть возможно больше и дольше, что зависит от подбора сорта пороха) примет некоторое среднее значение, которой будет соответствовать некоторая средняя скорость истечения газов из сопла и расход этого газа из сопла. Назовем через F среднюю силу, толкающую снаряд. (Черт. 152, 2-й снизу).
Тогда:
| |
|
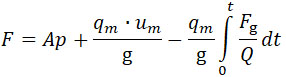 |
(41) |
Интегрируя это выражение по способу, указанному выше, получим:
| |
|
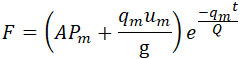 |
(42) |
Подставим значение F в:
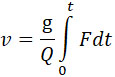
И после интегрирования получим:
| |
|
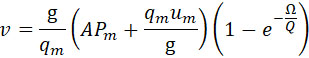 |
(43) |
Количество qm должно удовлетворять условию: qm = Ω (т- е. равняется весу заряда), где τ – время пробега снаряда в канале.
Предположим для простоты, что движение равномерно ускоренное. Тогда:
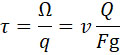
Подставляя значение F из (42), получим уравнение 1-ой степени относительно qm из которого имеем:
| |
|
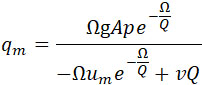 |
(44) |
р) Численный пример.
Формулы (43) и (44), очевидно, не имеют руководящего значения, так как они получены при приближенных допущениях. Однако, они указывают, до какой величины может достигнуть начальная скорость снаряда. Они дают возможность вычислить приблизительные размеры сопла при равных весах заряда и реактивного снаряда. Эти подсчеты подтверждаются опытами.
Обратимся опять к упомянутой выше пушке 152/45 с пониженной отдачей. Данные для нее следующие:
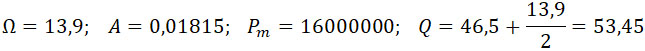
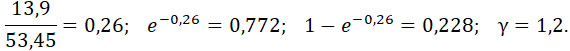
Предположим сорт пороха и прочность камеры таковыми, что допустима разность давлений внутри камеры и в канале – 1000 kg/cm2, так что Рm – 2600 kg/cm2.
По формуле (44) определим q = 900 kg/sec. По формуле (5):
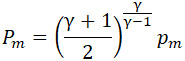
Поэтому:
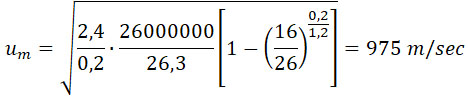
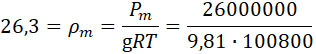
Из формулы (43):
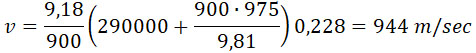
т. е. получается выигрыш в 14% в скорости и в 30%, в энергии, при равенстве заряда с таковым же в обыкновенной пушке.
Это преимущество еще более увеличится, если повысить разность давлений сверх 1000 kg/cm2.
Изложенная теория позволяет рассчитать размеры сопла снаряда.
q) Замечания относительно показателей и коэффициентов истечения.
В предыдущих подсчетах не были использованы коэффициенты сжатия при истечении газа, равно как и показатели истечения Цейнера. Поэтому неучтена и 3-я фаза, которая оказывает заметное влияние на начальную скорость. Показатель Цейнера не мог быть принят во внимание из-за отсутствия опытных данных и в том его значении, которое могло бы быть при малой разности давлений. Эти, интересующие нас данные, может дать только опыт.
Во всяком случае полученные приближенные результаты кажутся достаточными для оценки исследованных величин, тем более, что это подтверждено опытом.
r) Определение наибольшего давления в камере сгорания реактивного снаряда.
Может быть такой случай заряжания реактивного снаряда, при котором скорость полного газообразования заряда равна секундному расходу через сопло. Также возможен случай, когда плотность заряжания выражена тем же самым числом, которые выражает удельный вес взрывчатою вещества, т. е. когда в камере сгорания не остается места, свободного от вещества и доступного газам, которые должны, по мере образования, вырываться из сопла. В таком гипотетическом случае, который может быть лишь в начале взрыва, когда плотность заряжания для баллистита 1,6, наибольшее давление можно предугадать следующим образом.
Скорость (E) газообразования порохового зерна пропорциональна мгновенной его поверхности σ, плотности вещества и линейной скорости ω его воспламенения.
Эта скорость является функцией мгновенного давления и пропорциональна произведению линейной скорости горения на давление в n-ой степени.
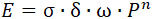
Если y есть отношепие между мгновенной толщиною зерна и половиною минимального размера зерна, и а, h, μ – характеристики его формы, v0 – его начальный объем, l1 – половина его минимального размера, то –
| |
|
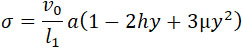 |
(46) |
Это выражение мы можем ввести в нашу формулу. Если заряд весом Ω содержит N зерен, то:
| |
|
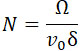 |
(47) |
Скорость полного газообразования будет:
| |
|
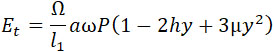 |
(48) |
Расход через сопло в секунду:
| |
|
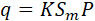 |
(8) |
Приравнивая Et и q, получаем искомую формулу, определяющую давление в нереальном случае, когда объем камеры сжимается во время горения, так что плотность заряжания остается постоянной:
| |
|
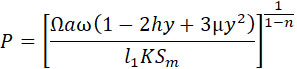 |
(49) |
Нам достаточно знать, для определения мощности снаряда, максимальное давление в камере сгорания. Для зерен обычной формы в виде нитей или брусков прямоугольного сечения имеем: μ = 0.
В этом случае, который является обычным, максимальное давление, при равенстве всех остальных условий, будет в начале явления, когда у = 0. Это давление при плотности заряжания 1,6 будет:
| |
|
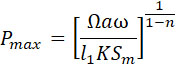 |
(50) |
Если плотность заряжания будет меньше 1,6, то и максимальное давление будет меньше того, которое определяется по (50), и тогда в нее необходимо ввести фактор, учитывающий эту плотность, что подтверждается и опытами. Здесь под плотностью заряжания подразумевается отношение веса заряда, находящегося в камере сгорания, к весу заряда, целиком заполняющего камеру. Предположим для простоты, что функция плотности заряжания является линейной, тогда сравнение результатов опыта и результатов подсчета по нижеприведенной формуле указывает на величину, отличную от тех, которые даются авторами трудов по внутренней баллистике обыкновенной пушки.
Формула автора имеет вид:
| |
|
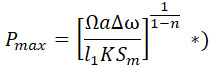 |
(51) |
В этой формуле:
Ω – вес заряда в kg.
Δ – относительная или объемная плотность заряжания.
ω – линейная скорость сгорания, при P = 1 равная около 0,002.
l1 – половина минимальной толщины первичного зерна (метр.).
K – в среднем 0,0065.
Sm – площадь в cm2 минимального сечения сопла.
a – имеет следующие значения для разных зерен:
нити или полоски 1x1............ a = 2
двойные полоски................... а =1,5
тройные.................................. а = 1,33
четверные.............................. а = 1,2
десятиричные........................ а = 1,1
листки..................................... а = 1.
п = 0,56.
Подставляя основные числа в формулу, получим:
| |
|
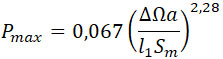 |
(52) |
В частном случае при
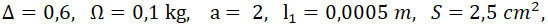
получим.
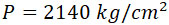
s) Обычные снаряды, выбрасываемые без отдачи легкой пушкой с обычными начальными скоростями.
Хотя предыдущие рассуждения и указывают на возможность получения начальных скоростей реактивного снаряда от 300 до 400 m/sec без значительного веса заряда, однако нижеследующее предложение могло бы иметь большое значение для вооружения аэрокораблей.
*) Из этой формулы следует, что величина показателя п=1, принимаемая большинством авторов для упрощения представления о скорости горения, не допустима. Действительно, при n=1 следует Р = ∞, что невозможно. Из той же формулы видно, что при Sm = 0, Р = ∞, что также невозможно (взрыв в замкнутой камере).
В этом случае следует вместо формулы (8) в подсчеты ввести выражение, зависящее от характеристического уравнения газов-продуктов сгорания, в котором фигурировал бы объем горючего.
Возможно ли на практике метать обычные снаряды с начальными скоростями от 700 до 800 m/sec без значительной отдачи и из легкой пушки?
Обычные снаряды имеют следующие преимущества перед удлиненными с собственной камерой сгорания.
1. Точность рассверловки.
2. Точность траектории.
3. Большая действительность поражения снарядом, так как в реактивном снаряде камера сгорания, летящая со снарядом, бесполезно поглощает часть его кинетической энергии.
Означенной цели можно достигнуть при помощи следующего устройства (черт. 152 внизу) пушки без отдачи. Пушка имеет канал, открытый с обоих концов (m/m).
Внутри пушки может двигаться трубка nn, с перегородкой (Р) посредине. В задней части трубки, за перегородкой, помещается заряд (a) и сопло (q). Снаружи трубки имеется ведущая нарезка для вращения во время пробега вдоль канала. Спереди перегородки помещается заряд (b), а перед ним снаряд, который имеет так же нарезы для вращения, когда он будет зарядом b выбрасываться из трубки n. Выстрел производится следующим образом:
Сначала взрывается заряд a и внутренняя трубка-пушка скользит вправо, как реактивный снаряд, внутри наружной пушки. Когда она дойдет до конца наружной пушки, взрывается второй заряд (b). Тогда снаряд вылетает из внутренней пушки, а последняя, под влиянием отдачи, возвращается в прежнее положение, по возможности плавно и без толчков.
Применение подобного принципа к обычным пушкам позволит метать снаряды на сотни километров. Однако, предпочтительнее применять наибольшие начальные скорости для действительности стрельбы с пологими траекториями.
t) Заметка о внешней баллистике снарядов, метаемых с аэрокараблей.
Вопрос о полете снаряда, метаемого с большой высоты (с аэрокорабля), является более сложным, чем при полете его при стрельбе из земной пушки. Усложнение происходит благодаря подвижности самого аэрокорабля в трех направлениях осей координат, и колебанию его около этих осей, не говоря уже о влиянии сноса корабля ветром. Даже и при обычной земной стрельбе вычисление траектории снаряда представляет значительные трудности и нет точного решения получаемых дифференциальных уравнений.
Даже Сиакки оставил ряд вопросов этого рода не разрешенными.
Для нашего случая, можно, однако, было бы применить для решения уравнений метод проф. Паскаля, построившего интеграф и предложившего способ вычерчивания траектории. Подобный прибор, дополняющий таблицы стрельбы, мог бы способствовать разрешению поставленного вопроса.
u) Заключение.
На основании всего вышесказанного можно заключить, что уже в ближайшем будущем на аэрокораблях могут устанавливаться орудия, выбрасывающие снаряды весом до 1000 kg со скоростью 400 и более m/sec с большой высоты. Сопротивляться этим снарядам с земли и с воды будет невозможно при помощи обычных средств защиты.
v) Заметка инженера Д. А. Крокко по поводу работы Пенья.
Инженер Д. Крокко поместил в журнале «Rivista aeronautica» 1926 г. № 3 статью, в которой он указывает на расходимость полученных Пенья выводов с его собственными. Однако, эта расходимость, по мнению Крокко, идет не в ущерб, а в пользу заключений Пенья.
Приводим содержание статьи Крокко.
* * *
Рассмотрим случай реактивного снаряда Пенья и применим те же обозначения:
r – реакция.
q – секундный расход заряда.
g – ускорение силы тяжести.
u – скорость извержения газа.
v – скорость движения снаряда.
m = q/g – масса, выбрасываемая в секунду из камеры,
M – масса снаряда, включая заряд в момент t.
M' – " " " " t + dt.
– dM = mdt – масса изверженного вещества за время dt.
Очевидно, что М' = М + mdt.
Для определения силы реакции, напишем уравнение количеств движения для моментов t и t+dt.
1. Для момента t: M'v или (M+mdt) v
2. Для момента t+dt: М (v + dv) + mdt (v + u)
Приравнивая эти выражения, получим:
Mv + mvdt = Mv + Mdv + mvdt + mudt
или,
Здесь u имеем знак противоположный v.
Уравнение (1) указывает на наличие реакции r, благодаря которой значительно возросла скорость dv массы М. Эта реакция равна:
Эта величина отличается от таковой же, полученной Пенья по уравнению (13), тем, что не зависит от v.
* * *
Этот результат, совпадающий с выводами Рябушинского, не представляется неожиданным. Масса mdt несется в пространстве с абсолютной скоростью u + v, но так как она обладала уже скоростью v вдоль пути снаряда, то она будет иметь относительную скорость u, от которой и зависит сила реакции.
Действительно, реакция r зависит от равнодействующей давления газа в камере сгорания, которые не уравновешены, благодаря наличию сопла, из которого газы могут выходить.
Благодаря этому и остаются давления, толкающие снаряд. На эти давления, очевидно, не влияет скорость снаряда v, которую и можно игнорировать.
Совсем другой случай представляется при работе двигателя, который толкает массу окружающей среды. Если эта масса неподвижна в пространстве и прибор имеет скорость v, то в этом случае реакция уменьшается на mv.
В реактивном же снаряде, где извергаемая масса вся заключается в самом снаряде и в момент t имеет уже скорость упомянутое уменьшение вводить нельзя
* * *
Если u – постоянно, то и r = const. Тогда скорость снаряда просто определяется уравнением:
Mdv = – mudt = udM,
откуда
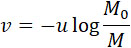
Это выражение, заменяющее таковое же (24), полученное Пенья, дает большую начальную скорость и благоприятствует выводам Пенья и дает в числовых примерах лучшие результаты.
В заключение упомянем, что данная нами формула приводит к результатам, кажущимся парадоксальными, именно, что скорость снаряда v может сравняться и даже превзойти скорость извержения, и если выбрать соответственное отношение 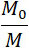 ; действительно при log ; действительно при log 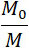 = 1, т. е. когда M0 = 2,71 т, v = – u. При этом вес заряда равен 0,631 полного начального веса снаряда. Теоретически говоря, можно получить любое значение v при данном u. Однако, при этом масса M0 будет сильно возрастать и конечная масса снаряда будет весьма мала по сравнению с начальной. = 1, т. е. когда M0 = 2,71 т, v = – u. При этом вес заряда равен 0,631 полного начального веса снаряда. Теоретически говоря, можно получить любое значение v при данном u. Однако, при этом масса M0 будет сильно возрастать и конечная масса снаряда будет весьма мала по сравнению с начальной.
* * *
|