|
Глава VII. Реактивный метательный снаряд.
Соч. Антонио де-Стефано.

В журнале «Rivista di Artiglieria e Genio» (Setternbre – Ottobre 1926, рg. 1611) была помещена статья генерала Антонио де-Стефано, под заглавием «Реактивный снаряд» (Il proietto a reazione).
Ниже излагается перевод этой статьи 1).
Современная ракета обладает малой меткостью. Хотя артиллеристы предложили ряд способов сделать ее более меткой, но успеха в этом отношении не достигли.
Хотя вращение снаряда повышает меткость, однако ранее для ракеты такого вращения достигнуто не было 2)
Теперь же имеются средства пустить и вращающуюся ракету, придав ей соответственную форму и назвав ее реактивным снарядом.
Мысль, – выбрасывать из нарезной пушки, открытой с казенной части, снаряд, движущийся в пушке и вне ее при помощи сгорающего заряда находящегося в самом снаряде – не нова. Ею занимались, например, Компанелли и Леджиардо. Последний, применяя принцип ракет, производил опыты с 75 mm пушкой. Добиваясь уменьшения отдачи, он проделал в затворе несколько отверстий для выхода газов, но в результате получилась слишком малая скорость снаряда. С увеличением заряда, увеличивалась отдача, с увеличением количества отверстий уменьшалась начальная скорость снарядов. Действуя таким путем, он дошел до момента, когда увеличение заряда становится опасным для того, кто стоял позади орудия.
В настоящей статье, я намерен рассмотреть, каких результатов можно ожидать на практика от реактивного снаряда, каковы должны быть полный вес снаряда и вес заряда, какова должна быть наилучшая нарезка, какие можно получить скорости и т. п.
Я ограничился случаем уже рассмотренным Пенья и Крокко, когда реактивный заряд сгорает целиком или почти целиком, внутри пушки, так что не приходится принимать в расчет влияние сопротивления воздуха и силы тяжести на скорость, сообщаемую снаряду реактивным действием газов.
Скорость снарядов. Представим себе реактивный снаряд, состоящий из обыкновенного метательного снаряда и из трубки с соплом, содержащей заряд, плотно помещенный в ней в задней части снаряда.
1) Перевод этот сделанный Е. В. Агокас появился в журнале «Война и Техника» №2 4, 1927 г. Нами также был сделан этот перевод. Но ввиду того, что впервые он был опубликован Агокасом, мы приводим этот последний с незначительными корректурными изменениями и примечаниями.
2) Автор очевидно говорит лишь о ракетных артиллерийских снарядах, так как обычные ракеты уже устраиваются вращающимися (например, но патентам Годдара).
Пусть gM – вес всего снаряда, т. е. вместе с реактивным зарядом, и пусть gm вес газов, выбрасываемых в секунду. Начнем счет времени с момента воспламенения заряда, и пусть v скорость снаряда к моменту времени t и u 3) (считаемая положительной в направлении выхода газов) – скорость истекающих газов относительно снаряда.
3) А. де-Стефано обозначает η своей статье эту скорость то через (U), то через (u). Мы, как и Агокас, сохраняем постоянное одно обозначение u.
Количество движения снаряда, за исключением массы mdt взрывчатого вещества, которое должно преобразовываться в газ в течении времени dt, во время t будет (M – mt – mdt) v, а во время t + dt будет (M – mt – mdt) (v – dv). В течение времени dt преобразуется в газ упомянутое количество взрывчатого вещества mdt, которое во время t имеет скорость v, а во время t + dt скорость v – u.
Если отсутствуют силы, действующие на снаряд и на газы, т. е., если мы не принимаем в расчет сопротивление воздуха, силу тяжести и другие второстепенного значения, то получим: (M – mt – mdt) (v + dv) – (M – mt – mdt) v для снаряда, и m (v – u) dt – mv dt – для заряда.
Или:
(M – mt – Mdt) (d + dv) – (M – mt – mdt) v + m (v – u) dt – mv dt = O.
Откуда, сокращая и пренебрегая бесконечно-малым высшего порядка, получим:
(M – mt) dv = mudt.
Интегрируя в пределах времени от O до t, получим:
| |
|
|
|
|
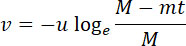 |
|
|
(1) |
Если приходится принимать в расчет сопротивление воздуха и силу тяжести, то обозначая через Θ угол наклона касательной к траектории к горизонту в момент t, получим уравнения проекций сил на две оси координат:
(M – mt) d (v cos Θ) – mu cos Θ dt = – (M – mt) f (v) cos Θ dt (2)
(M – mt) d (v sin Θ) – mu sin Θ dt = – (M – mt) f (v) sin Θ dt – g (M – mt) dt (3)
Умножим уравнение (2) на v sin Θ, а уравнение (3) на v cos Θ, вычтем почленно одно из другого и разделим на v2 cos2 Θ, тогда получим:
| |
|
|
|
|
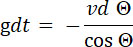 |
|
|
(4) |
Подставляя эту величину в уравнение (2), получим уравнение годографа:
| |
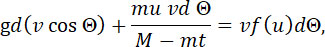 |
|
|
(5) |
которое отличается от уравнения баллистики обыкновенных снарядов прибавлением члена
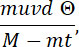
Последний уничтожается при u = О, и тогда уравнение (5) приводится к обыкновенному уравнению баллистики. Подставляя найденную величину dt в выражения:
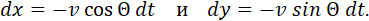
получим:
| |
|
gdx = — v2 dΘ и gdy = — v2 tg Θ d Θ. |
|
(6) |
Уравнения (6) и (4) не отличаются от обычных уравнений баллистики, но значения х, у и t – иные, при одинаковых параметрах, определяющих траекторию, поэтому и величина скорости, определяемой уравнением (5) будет иная.
Заканчивая этим рассмотрение вопроса в более общем случае, переходим к исследованию частного случая.
Введем обозначения:
A – площадь поперечного сечения сопла, в котором скорость истечения газов — u.
u – скорость истечения газов.
δ – плотность газа в момент прохождения его через указанное сечение сопла.
δ0 – плотность взрывчатого вещества.
δ1 – плотность газа в камере сгорания.
q – часть заряда, сгоревшая в течение времени t.
ω – вес реактивного снаряда.
W – объем камеры сгорания реактивного снаряда,
α – коволюм взрывчатого вещества.
f – сила взрывчатого вещества.
P – давление во время t.
γ – показатель политропы при адиабатическом расширении газов.
w – скорость сгорания зерна заряда при постоянном (unitaria) давлении.
2l1 – толщина зерна.
y – часть толщины зерна, сгорающая за время t.
T – Температура сгорания.
R – газовая постоянная.
Давление внутри камеры. Принимая во внимание, что вес газа, вытекшего из трубки с самого начала за время t, равен
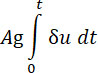
и что в уравнении Нобля вес этот вычтен из части ωq сгоревшего заряда, и потому он более не участвует в изменении давления, получим:
| |
|
|
|
|
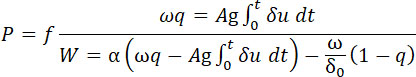 |
|
|
(7) |
Скорость истечения при атмосферном давлении определяется уравнением
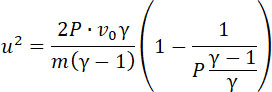
Здесь v0 – объем (за вычетом коволюма) весовой единицы газа и m = 1/g масса того же газа в камере сгорания.
Пренебрегая коволюмом, примем
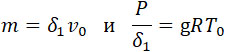
В отношении последней формулы предполагаем, что газы, несмотря
на легкое расширение, при котором выполняется небольшая работа, находятся в камере при температуре T0. В то же время, при допущении
расширения газа при выходе по адиабате, получим:
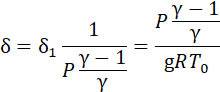
Скорость истечения будет:
| |
|
|
|
|
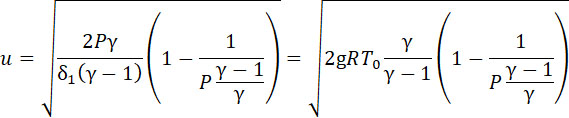 |
|
|
(8) |
в результате
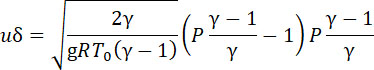
Известно, что сгоревшая часть заряда определяется формулой
| |
|
|
|
|
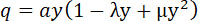 |
|
|
(9) |
Предположим, что скорость сгорания изменяется пропорционально
первой степени (prima potenza) 1) давления (известно, что опыты не дали
единой величины этого показателя); тогда получим:
| |
|
|
|
|
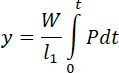 |
|
|
(10) |
Подставляя это значение y в (9), и величины δu и q в (7), получим
дифференциальное уравнение, связывающее P и t, из которого можно
определить P в зависимости от t.
Зернистость взрывчатого вещества. Особое внимание мы
обращаем на то, чтобы P не превосходило данной величины Pm с тою
целью, чтобы не превзойти сопротивления, допускаемого для стенок
камер реактивного заряда. Для того, чтобы получить больше скорости
снаряда, необходимо, чтобы P сохраняло приблизительно максимальную
величину, принятую для Pm во время сгорания заряда, так как согласно
уравнению (1) скорость снаряда повышается с (u), а из (8) – (u) – увеличивается с P.
Необходимо, чтобы P возросло в кратчайший срок до величины Pm
и сохраняло эту величину до конца сгорания заряда. Газ, который
остается в камере, выйдет одновременно с быстрым понижением P.
1) Агокас переводит это выражение «первоначальная сила». Из уравнений (7, 8, 9, 10) можно вычислить значение P для любого
момента; однако, величины P в начале и конце оказывают малое влияние на скорость снаряда. Если поставить условие, что количество газов вытекающих при давлении P = const, равно количеству газов образующихся, то должно быть:
| |
|
|
|
|
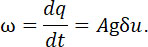 |
|
|
(11) |
или:
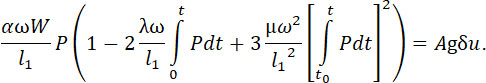
Здесь t0 – время, момент, когда это соответствие начало осуществляться.
Чтобы это имело место независимо от времени, необходимо, чтобы
μ = λ= O, каковому условию удовлетворяют пластинки и длинные
трубки с отверстиями; при этих трубках также a = 1.
Сечение сопла трубки. Из последнего уравнения имеем:
| |
|
|
|
|
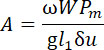 |
|
|
(12) |
при условии, что P = Рm и остается предельной, если l1 определено
по ниже приведенному уравнению (17).
Однако P не постоянно и в действительности нет строгого соответствия между и скоростью истечения и весом вытекающего газа в единицу времени, что видно из уравнения (7), так как по мере сгорания
заряда увеличивается свободный объем камеры. В результате получается
незначительное уменьшение скорости снаряда.
Применяя упомянутые формулы на практике, мы приходим к выводу,
что необходимо доводить заряд до полного сгорания вне пушки, потому
что иначе для A получилась бы величина гораздо больше той, которая
возможна быть допущенной.
Вес реактивного заряда, масса, выталкиваемая в единицу времени. Продолжительность сгорания.
Полагая s – путь, пройденный снарядом, и считая его s = 0 при t = 0
получим из (1):
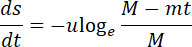
откуда, интегрируя:
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
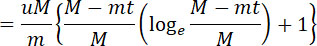 |
|
|
(13) |
Вообще начальная скорость будет υ и полный путь снаряда – L.
Из формулы (1) имеем:
| |
|
|
|
|
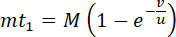 |
|
|
(14) |
Здесь t1 – время, употребляемое снарядом для достижения скорости v.
Из формулы (13) имеем:
| |
|
|
|
|
|
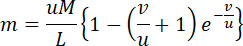 |
|
(15) |
и, отсюда,
| |
|
|
|
|
|
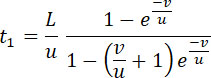 |
|
(16) |
Заметим, что gmt1 = ω и в результате, на основании (14), определяется, какая часть веса снаряда относится на заряд.
Толщина зерна. Толщина пластины или трубки пороха дается
формулой
| |
|
|
|
|
|
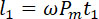 |
|
(17) |
Объем камеры. Величина W в формуле (12) может быть любая, что
оправдывается следующими соображениями: какова бы не была величина
Wt лишь только газы достигают давления Pm, входящего в уравнение (12),
количество газов, образовавшееся от сгорания, равно, по (11), количеству вытолкнутых газов и, следовательно, давление не может возрастать.
В зависимости от величины W изменяется время (определяемое по (7),
которое требуется, чтобы газы достигли давления Pm.
Полный вес снаряда. Пусть Pm – давление внутри реактивной
камеры, D – калибр снаряда, равный внешнему диаметру трубы, образующей камеру, D1 – внутренний диаметр ее. Тогда имеем:
| |
|
|
|
|
|
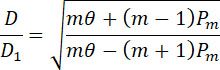 |
|
(18) |
Положим m = 3. Тогда получим толщину стенки по величине скорее
больше действительной, чем меньшей.
Пусть l – длина трубки с зарядом, удельный вес стали 7,8. Вес трубки
будет:
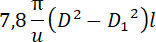
Пусть p – вес снаряда, выбрасываемого из современных пушек, gM вес
всего снаряда и 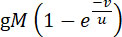 – вес всего заряда. Тогда: – вес всего заряда. Тогда:
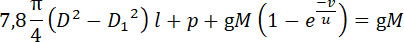
Внутренний объем трубки 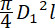 . Предположим, что только часть
ее (напр. 4/5) занимается зарядом с удельным весом 1,6, тогда . Предположим, что только часть
ее (напр. 4/5) занимается зарядом с удельным весом 1,6, тогда
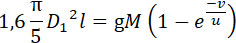
откуда:
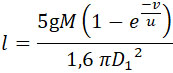
Подставим это значение l в предыдущее уравнение:
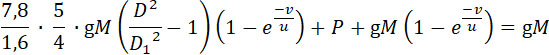
откуда:
| |
|
|
|
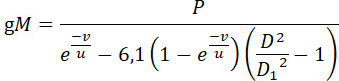 |
|
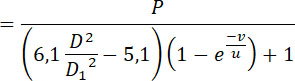 |
|
(19) |
Величина D / Dt получается из (17), (u) – из (8). Поэтому уравнение (19)
дает вес gM всего снаряда.
Возьмем производную по P знаменателя формулы (19):
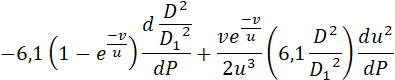
Так как 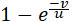 и и 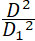 больше нуля, больше нуля, 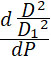 по формуле (18)
также больше нуля, а по формуле (18)
также больше нуля, а 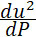 по (8) меньше нуля, то вся производная отрицательна; это показывает, что знаменатель P уменьшается, а величина gM увеличивается при увеличении P. по (8) меньше нуля, то вся производная отрицательна; это показывает, что знаменатель P уменьшается, а величина gM увеличивается при увеличении P.
В результате полезно, чтобы величина P была возможно меньше,
так как при этом уменьшается вес снаряда.
Одновременно с уменьшением P уменьшается (u), а это особенно
важно, потому что из формулы (8) вытекает, что даже при очень низких
давлениях величина (u) остается высокой (см. напр. работы Пенья и его
диаграммы).
Приложения. Сделаем некоторые применения изложенного. Определим, например, вес реактивного заряда с начальной скоростью 500 m/sec,
калибра 75 mm и при весе снаряда 6.5 kg.
Пусть максимальное давление в трубке с зарядом будет Pm = 100 атмосфер, сталь трубки с пределом упругости Θ = 40, L = 1,5 m, u = 2200 m.
Тогда из (19) имеем:
gM = 8,85 и ω = gmt1 = 1,787,
τ. е., заряд должен быть в 4 раза больше того, который необходим
в обыкновенных пушках, чтобы получить тот же самый эффект.
Однако, если мы вычислим величину сечения A для этого случая,
то заметим, что выход всех газов из снаряда, получающихся от сгорания
всего заряда, невозможен в течение короткого времени пробега снаряда
в пушке.
Если:
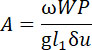
и так как из формулы (17) получается l1 = ωPt1 и ω = gmt, то при подставке имеем:
| |
|
|
|
|
|
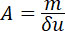 |
|
(20) |
Относя P на m2, получим:
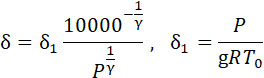
что мы имели и раньше. Подставляя P = 30, T = 3200, Pm = 1000000,
γ = 1,4, получим δ = 0,037.
Из (15) получаем m = 26,6 и отсюда A = 0,325 m2, т. е. отверстие
сопла трубки, заключающей реактивный заряд, должно быть гораздо
больше, чем максимальная величина π/4 D12.
Очевидно, надо увеличить длину L, т. е. заряд должен продолжать
гореть даже после того, как снаряд вылетел из пушки, но чтобы найти,
какова должна быть величина L, выведем ее из (20), полагая А = π/4 D12.
Произведя подсчеты, получим:
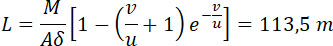
т. е. заряд перестает гореть, когда снаряд удалится свыше 100 метров.
При этой новой величине L имеем m = 0,356.
Таким образом невыгодно, когда A становится слишком большой,
брать для γ величину меньше 1,4 или повышать Pm, так как величины
δ и u мало изменяются и одновременно M изменяется в том же направлении, как и δ. Следует заметить, что величина gM при возрастании Pm, возрастает настолько, что быстро принимает невозможные значения,
делаясь отрицательной и обращаясь в бесконечность.
В нашем случае вес снаряда делается бесконечно большим для Pm
не свыше 750 атмосфер. За пределами известной величины P толщина
трубы становится такой, что во внутренней пустоте уже не может помещаться часть веса снаряда, составляющая заряд – 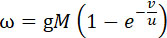 и поэтому, при удлинении трубы с целью увеличить вес за заряда, получается в результате увеличение веса снаряда. Следовательно, с того
момента, когда является необходимость, чтобы сгорание заканчивалось
по вылете снаряда на траектории, требуется знать, сообщает ли снаряду
достаточную скорость вращения та часть заряда, которая сгорает в пушке
к моменту вылета. и поэтому, при удлинении трубы с целью увеличить вес за заряда, получается в результате увеличение веса снаряда. Следовательно, с того
момента, когда является необходимость, чтобы сгорание заканчивалось
по вылете снаряда на траектории, требуется знать, сообщает ли снаряду
достаточную скорость вращения та часть заряда, которая сгорает в пушке
к моменту вылета.
Из (13) можно получить 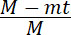 а из (1) – ν. Произведя вычисление,
получим весьма малую скорость. а из (1) – ν. Произведя вычисление,
получим весьма малую скорость.
Мы окажемся не в лучших условиях, если пожелаем сообщить тому же
снаряду скорость 1500 т. Тогда он должен весить 19 kg, а заряд 7,84 kg.
Однако, при этом невозможно практически удовлетворить значению A.
На основании предыдущего, мы получим, что снаряд должен гореть по
выходе из пушки еще на протяжении почти 1,5 km, а скорость его
внутри пушки будет весьма малой.
Если пушка будет калибра 381 и снаряд весом 885 kg при скорости
700 т, то реактивный снаряд будет весом 1380 kg, с зарядом 375 kg, подобно тому, как и для 75 mm пушки, и скорость при вылете из пушки
будет очень мала и сгорание закончится на 1,5 km по вылете из пушки.
Заключение. Из полученных результатов можно сделать вывод,
что невозможно выбрасывать снаряд, по крайней мере в рассмотренных
случаях, доводя сгорание реактивного заряда до конца к моменту вылета
снаряда из дула пушки и невозможно также сообщить снаряду вращение
за счет той скорости, какую снаряд развивает внутри орудия.
При стрельбе на суше или на море вращение можно сообщить посредством выталкивающего заряда, который обыкновенно весит немного.
При стрельбе с самолетов следует действовать иначе.
В заключение следует заметить, что если на опыте окажется, что
меткость не слишком страдает, то эти снаряды, несмотря на сравнительно большой вес, большую длину и большую трату взрывчатого вещества, все же, во многих случаях, могут оказать существенные услуги.
* * *
|