|
g) Замечание о 3-ей фазе.
3-я фаза аналогична работе ракеты с пневматическим зарядом внутри него. Такой снаряд состоит из стальной трубы, закрытой с одной стороны, а с другой снабженной дюзой и соплом. У заднего конца его имеется стабилизатор, а внутри находится воздух, сжатый до 40 атмосфер.
В нашем случае вместо сжатого воздуха находится газ от горючего под давлением P и при температуре – Т.
Теория этого случая дана Д. Рябушинским в выпуске VI трудов его Института. Эта теория, основанная на законах истечения газов, дает довольно простые результаты, однако автор не учитывает уменьшение количества движения истечения газов, происходящее благодаря скорости движения ракеты. Дифференциальные уравнения, получаемые из таковых же Рябушинского, при введении этой поправки, не легко интегри руются, так как величина 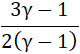 не целое число. Поэтому проще изобразить функцию графически и интегрирование производить механически. не целое число. Поэтому проще изобразить функцию графически и интегрирование производить механически.
Значительное упрощение в теории можно получить, если в предыдущие формулы вместо переменных u, q и т. п., взять их средние значения, что, повидимому, дает результаты довольно надежные.
Из черт. 151d следует что энергия, заключающаяся в единице веса газа находящегося первоначально в камере сгорания в 3-й фазе, пропорциональна площади, ограниченной кривой и осями координат. Эту площадь можно заменить равновеликой ей площадью, прямоугольника, основание которого – конечный удельный объем расширяющегося газа, а высота – среднее давление Pm.
Искомая площадь равна; (черт. 151 d).
| |
|
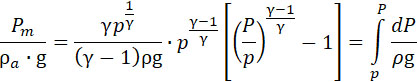 |
(31) |
откуда
| |
|
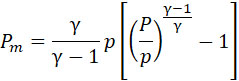 |
(32) |
Обращаясь к формуле (5), из которой выведена 8bis, можем определить средний расход газа через сопло за 3-ю фазу:
| |
|
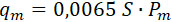 |
(33) |
Подставим это значение в формулу (13), где (u) определяется по (14), а р = Рm. Тогда из (13)
| |
|
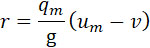 |
(34) |
Подставляя (34) в (17), получим:
| |
|
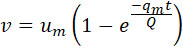 |
(35) |
Произведение qm • t в конце 3-й фазы эквивалентно весу, который мы обозначим через ω. Формула (35) составлена в предположении, что скорость снаряда в начале 3-й фазы равна 0. Эта формула совпадает с (29). Аналогично (30) можно составить формулу, определяющую пройденный путь.
Эти формулы можно непосредственно применить к пневматической ракете. Обращаясь к числовому примеру, данному Д. Рябушинским в его бюллетене, получим скорость не 114,5 m/sec, а 114,2 m/sec.
В случае, который нас интересует, снаряд в начале 3-й фазы обладает уже начальной скоростью v.
Скорость снаряда в конце 3-го периода определяется по способу, аналогичному ранее приведенному, и равна
| |
|
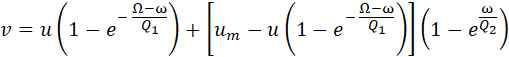 |
(36) |
где
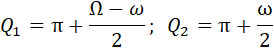
Эта формула аналогична (29). Показатель в первом члене по абсолютной величине гораздо больше такового же во втором члене и скорость (u) значительно больше скорости во втором члене. Поэтому можно пользоваться простой формулой (29), не делая большой ошибки в последующих числовых примерах.
h) Числовые примеры.
Обозначим через V объем камеры сгорания. Согласно принятым обозначениям имеем:
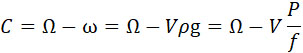
Для последующего расчета обратимся к формуле (36). Пусть вес снаряда Q1 = 100 kg, – заряда Ω = 25 kg (баллистит). Примем P = 1000 kg/cm2. Из графика u = 2440 m/sec. Полагаем f = 108000 и плотность заряжания = 1. Тогда:
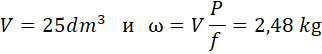
Из формулы для Q1 получим:
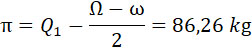
Для 1-го члена формулы (36) имеем
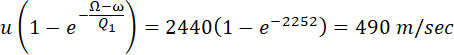
Второй член формулы (36) получит вид:
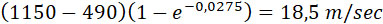
Этот результат вполне оправдывает то, что мы принебрегли вторым членом формулы (36) для предварительных подсчетов реактивного снаряда.
На черт. 151е нанесены начальные скорости реактивного снаряда при среднем давлении Р = 1000 kg/cm2 и при плотности заряжания = 1. Это можно допустить для случая, когда узкое сечение сопла имеет достаточную площадь *).
Для других случаев расчет производится подобно выше приведенному.
*) Можно доказать, что при одном и том же заряде отношение энергии, сообщенной для метания реактивного снаряда, к такой же для снаряда обыкновенной пушки при равных весах равно 0,66. На черт. 151-е линейчатым крупным пунктиром изображена опытная кривая при начальной скорости, полученной со снарядами, выбрасываемыми обычной пушкой. На практике коэфф. полезного действия реактивного снаряда несколько больше 0,66 по сравнению с обычной пушкой (с коэффициентом 1), так как в этом случае потери энергии гораздо меньше, чем при обыкновенном снаряде. Коэффициент полезного действия пушки Дэвиса равен около 0,5 по сравнению с обыкновенной пушкой (коэффициент которой принят за 1).
i) О нарезке открытой пушки с реактивным снарядом.
Обозначим через Θ наклон нарезки постоянного шага, через Z – полную силу, действующую | к оси канала (по касательной), через d – средний диаметр нарезки, через M – вращательный момент снаряда, через φ – коэффициент трения. Тогда инеем (черт. 151f):
| |
|
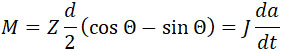 |
(37) |
Здесь J – момент инерции снаряда относительно его оси, a – угловая скорость снаряда относительно той же оси.
Далее:
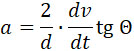
Из (37) получаем:
| |
|
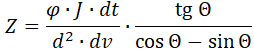 |
(38) |
Но
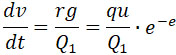
поэтому:
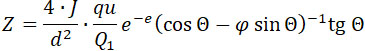
Эту формулу мы должны применять при проектировании орудия. Принебрегая влиянием трения газов, вырывающихся из снаряда во время его движения в канале орудия, что трудно поддается анализу, получим, что сила отдачи в реактивной пушке определяется формулой:
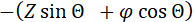
Вращающий эффект, действующий при выстреле на орудие, нейтрализуется реакцией цапф и равен и противоположен моменту M (форм. 37).
Заметим, что сила, названная нами отдачей, направлена вперед и возникает благодаря трению между нарезами и каналом. Эта сила весьма мала, как это видно из последующего примера. В нашем случае нарезы сделаны прямоугольного сечения и стальной поясок снаряда имеет нарезные зубцы. Можно совершенно уничтожить силу отдачи, снабдив снаряд вспомогательными трубками, дающими потенциальную отдачу обратного знака, которую можно подсчитать и которая аннулирует силу Z.
j) Числовой пример, относящийся к расчету нарезки и отрицательной отдачи (калибр 190 mm).
Ранее был рассмотрен снаряд калибра 190 mm. Узкое сечение сопла имело диаметр 150 mm, сечение S = 177 cm2. Этим данным соответствовал секундный расход газа:
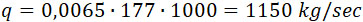
Скорость истечения u = 2440 m/sec.
Средний вес снаряда 100 kg, величина с = 0,2252.
Приняв начальную скорость равной таковой же при гаубице, положим
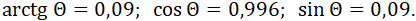
Коэффициент трения стали по стали при хорошей полировке примем 0,15.
Момент энерции снаряда относительно продольной оси J = 0,063. Высоту зубцов нарезки примем 4 mm, тогда d = 0,194 m.
Получаем:
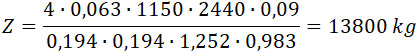
Сила отрицательной отдачи равна:
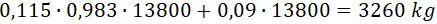
Такая отдача уже допустима для самолета весом 10000 kg. Но мы видели уже, как ее можно аннулировать.
Вращательный момент, передаваемый каналу орудия, равен:
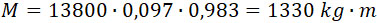
И этот момент можно аннулировать при помощи вышеупомянутых трубок.
Определим теперь, какова должна быть длина канала орудия, чтобы в нем закончилась вторая фаза.
Из (30) получаем:
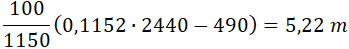
т. е. Длина пушки равна 27,5 калибрам, но следует ее делать около 30 калибров, чтобы направить снаряд и в первой части З-й фазы.
k) Заметка об обыкновенных снаряде и пушке.
Из общей механики жидкости известно, что при скорости истечения газа u и секундном расходе его q, давление на неограниченную плоскость, нормальную к потоку будет:
| |
|
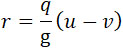 |
(40) |
где v — скорость движения этой плоскости, перемещающейся в направлении (u). Это позволяет сделать переход к формуле (13), относящейся к реактивному снаряду.
Таким образом, если приходится изучать движение массы, соединенной с поверхностью, получившей толчек, то можно применять формулы, идентичные с выведенными. Черт. 151g представляет орудие обыкновенного действия. Все вышесказанное можно было бы приложить к этому случаю лишь при условии, что газовая струя оставалась бы сжатой (сечение и скорость постоянны во все время действия на днище снаряда, что невозможно) и что площадь днища бесконечно велика, или имела такую величину, чтобы струйки газа направлялись, как показано на черт. 151h.
Так как эти условия практически не осуществимы, то необходимо добавить множитель, меньший единицы во втором члене формулы (40).
Коэффициент полезного действия обычной пушки будет во всяком случае меньше, чем реактивной.
l) Акционный снаряд, введенный в трубку.
На черт. 152 вверху изображен акционный (выталкиваемый газами, получающимися извне снаряда) снаряд, заключенный в трубу.
В этом случае газы не могут идти, как показано стрелками на черт. 151h, и не могут распространяться радиально. Поэтому в трубе возникает статическое давление, и здесь не может быть речи об акционном снаряде.
Если струя газа малого сечения относительно сечения канала трубы действует на днище снаряда, то получается картина на черт. 152, 2-й сверху. Однако в этом случае, в зоне пограничной между прямым и обратным потоками, получатся такие вихри, что нарушится правильное движение струй, и не будет достигнута скорость снаряда, предполагаемая теорией.
В случае, показанном на черт. 152 сверху, можно принять, что внутри трубы образуется статическое давление, которое, отнесенное к единице площади, равно таковому же, когда поток свободного газа действует на основание изолированного снаряда.
Поэтому пушка с акционным снарядом не представляет никаких преимуществ с обыкновенной пушкой, и коэффициент ее полезного действия меньше такового же реактивной пушки, которая, в свою очередь, равен 0,66 такового же обыкновенной пушки.
Сила отдачи акционной пушки равна реакции при истечении газа из камеры сгорания, выраженной формулой (13), где v следует положить = 0.
Величина этой силы того же порядка, как и в эквивалентной обыкновенной пушке. Отдача теоретически аннулируется в случае по черт. 152 (две сверху), когда камера сгорания и труба жестко соединены друг с другом.
Черт. 151е дает приблизительное представление о начальных скоростях, получаемых с пушкой и акционным снарядом (турбо пушка), в зависимости от отношения веса заряда к весу снаряда. Из него можно сделать вывод, что при пушке с акционным действием для получения начальной скорости 1000 m/sec, отношение Ω/π должно равняться 0,54, т. е. при снаряде весом 50 kg заряд должен теоретически равняться 27 kg. Для получения подобной же скорости в обыкновенной пушке заряд равнялся бы 20 kg.
В акционных (турбо) пушках, для избежания больших размеров камеры необходимо применять более высокие давления, чем в обычных пушках, и обратно, при низких давлениях, придется увеличивать вес камеры, так как ее объем будет больше объема обыкновенной пушки.
Наконец, если желательно, для получения практического коэффициента полезного действия, равного теоретическому, заставить функционировать снаряд внутри канала (черт. 152 вверху) (при атом будет потеря энергии такая же, как и при обыкновенном снаряде), то труба должна испытывать давление на единицу поверхности почти такое же, как и в обыкновенной пушке.
Поэтому турбо-пушка не представляет никаких преимуществ по сравнению с обычной.
m) Обычные пушки без отдачи.
Ранее мы говорили о пушке Дэвиса, отдача которой уничтожается контр-снарядом, обладающим тем же количеством движения, что и сам снаряд. Очевидно, того же результата можно достигнуть в обыкновенной пушке, используя количество движения некоторой части газа высокого давления, вырывающегося из отверстия в направлении, обратном полету снаряда.
Пусть P' – полное давление на дно канала. Оно будет достаточно для получения реакции P', образующейся при выходе газа из упомянутых трубок.
Так как P' – A • P, где P – давление на единицу площади внутри канала, то достаточно, чтобы через отверстия вырывался тот же газ, который находится внутри пушки. Получающаяся при этом реакция, при постоянном на практике и, будет пропорциональна P и равна:
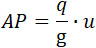
Здесь q, как мы уже видим, пропорционально P в фазе воспламенения, когда давление можно на практике принять постоянным и пропорциональным 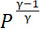 (т. е. пропорциональным P, так как γ, как полагают все авторы, невелико) в периоде расширения. (т. е. пропорциональным P, так как γ, как полагают все авторы, невелико) в периоде расширения.
На основании этих данных не представляет затруднений рассчитать отверстия и заряд для уничтожения отдачи и для получения требуемой начальной скорости.
После всего вышесказанного в предыдущем параграфе можно заключить, что турбо-пушка вполне соответствует рассматриваемому здесь случаю, но нужно лишь исключить эффект действия газов на дно ее. Такая пушка в отношении той же начальной скорости снаряда, соответствует обычной пушке, в канале которой устроены соответствующих размеров отверстия для отводов газов.
Принимая положение, что внутри канала пушки с пониженным давлением не может получиться динамическое давление на дно снаряда, а лишь статическое, имеем вывод, что среднее давление, необходимое для сообщения снаряду данной начальной скорости, должно равняться среднему давлению, необходимому для получения той же начальной скорости в обыкновенной пушке (при одинаковых весе снаряда и длине его пути в канале).
Как следствие, также вытекает, что заряд пушки с пониженной отдачей должен быть выше такового же в обыкновенной пушке, при равных весах снарядов и путей их в канале.
Ствол пушки должен иметь тот же вес, что и у обыкновенной, но зарядная камера ее будет тяжелее, больше и испытывать больше давления.
Пушка, о которой мы говорим, представляет попытку решения вопроса об уменьшении отдачи, но с точки зрения баллистики всегда возможно спроектировать обыкновенную пушку, которая при меньшем заряде, при давлении равном и даже меньшем, дает начальную скорость снаряду такую же, как и пушка с пониженной отдачей.
n) Расчет заряда для упомянутой пушки.
Чтобы отдать себе отчет, каково потребуется увеличение заряда, чтобы указанным способом аннулировать отдачу, была испытана пушка 152/45. Вес снаряда 46,5, заряда 13,9. Начальная скорость, при среднем давлении 1600 kg/cm2, была 830 m/sec. Для получения такой же скорости при пушке с пониженной отдачей, необходимо то же среднее давление. Заряд в такой пушке будет:
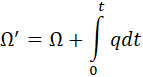
Для краткости и не уклоняясь от истины, можно вычислить q по теореме о средних величинах, выразив, что реакция сопла должна равняться части K силы отдачи, которую желательно устранить:
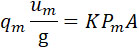
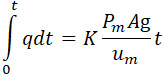
Величину t можно, с достаточным приближением, определить, полагая движение снаряда равномерно ускоренным при среднем ускорении:
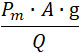
Обозначая через L длину пробега снаряда, получим время этого пробега:
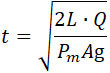
После подстановки, получим:
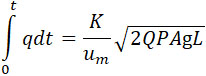
При 152 – L = 6 m, A = 0,01815 и γ = 1,2, получим u = 2900 m/s.
При полном аннулировании отдачи, т. е. при K = 1, получим:
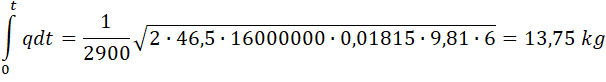
Итак, в рассматриваемой пушке для того, чтобы бросить снаряд со скоростью 830 m/sec, как в обычной пушке 152 с зарядом 13,9 kg, необходим заряд 13,9 + 13,75 = 27,65 kg.
Снаряд реактивного действия и турбо-пушка дали бы, при
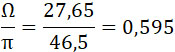
такую же начальную скорость (теоретически 1050 m/sec).
Уничтожение силы отдачи в обыкновенной пушке можно получить путем соединения камеры сгорания с соплами, направленными к казенной части и заряженными веществом, взрывающимся одновременно с зарядом в пушке.
Хотя подобные способы решения вопроса уничтожения отдачи и кажутся полезными в некоторых случаях, однако, их не следует применять на легких платформах, в роде тех, которые имеют место на моторных лодках и аэропланах.
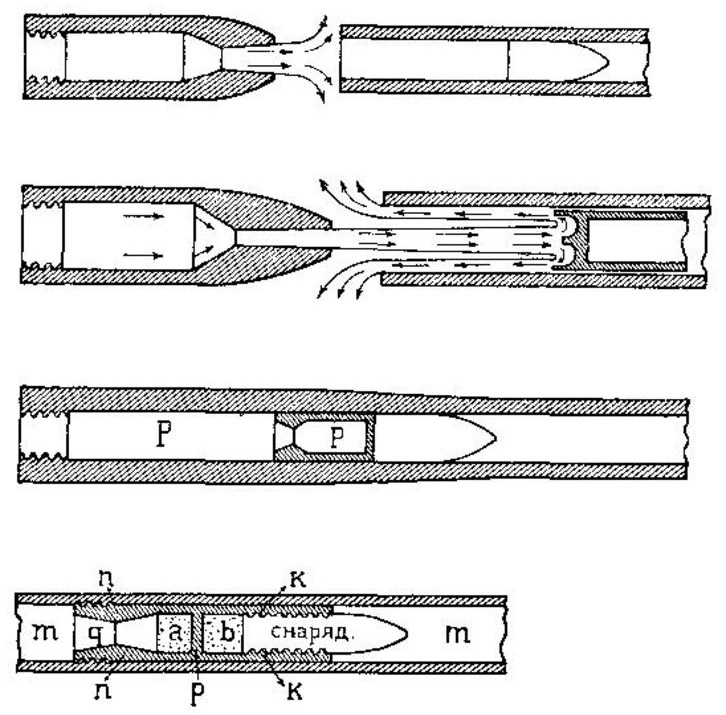
Черт. 152. Снаряды Пенья. |
|
|