|
Глава VI. Орудия крупного калибра
на воздушных судах.
Соч. Пенья Джиованни.
а) Предисловие.
Помещаемый ниже перевод статьи итальянского инженера Джиованни Пенья, хотя и озаглавлен автором, как трактующий об орудиях, однако, по существу, заключает в себе теорию реактивного снаряда и является в этом отношении развитием работы Д. Рябушинского. Статья Пенья была напечатана в итальянских журналах «L’ala d’ltalia» 1926 г. № 2 и 4 и «Rivista Aeronautical» 1926 № 1.
Русский перевод части этой статьи был помещен в журнале «Война и Техника» 1927 г, № 1.
Мы самостоятельно перевели статью Пенья, пользуясь упомянутыми двумя итальянскими журналами и добавили к ней критическую заметку инженера Крокко, помещенную в журнале «Rivista Aeronautica» 1926 г. № 3, составленную под влиянием работ Рябушинского и Эсно-Пельтри.
b) Открытая пушка с реактивным снарядом.
Применение на воздушных судах орудий большого калибра приводит к необходимости разрешения вопроса о пушках, отдача которых была бы сведена к минимуму.
Примером такой пушки может служить орудие Дэвиса, открытое с обоих концов. В середине ее помещается заряд, к которому примыкают; с одной стороны снаряд, а с другой мешечек с дробью (контрснаряд), масса которого равна массе снаряда. При выстреле получается равенство живых сил снарядов и фиктивного контр-снаряда, и отдача получается теоретически равна нулю.
Несмотря на это преимущество, применение пушки Дэвиса влечет за собой следующие неудобства: а) необходимость перевозить на аэрокорабле мертвый груз равный весу снарядов. b) опасность для соседнего самолета от контр-снаряда, c) значительные затруднения в заряжании, d) не полное использование обычной части энергии заряда, выталкивающей снаряд, e) для получения в пушке Дэвиса такого же давления газов, как и в обыкновенной, приходится увеличивать толщину стенок ее. При равенстве начальных скоростей снарядов, вес пушки Дэвиса, равнн почти удвоенному весу обыкновенной пушки. Поэтому пушки Девиса при облегчении их веса, будут давать малую начальную скорость, а это невыгодно для авиации.
Для избежания всех этих неудобств автором предлагается открытая пушка с реактивным снарядом и дается следующая теория этой стрельбы.
Меры выражены в kg, m, sec.
Обозначения приняты следующие:
t – время.
S – путь.
g – ускорение силы тяжести,
π – вес пустого снаряда.
Ω – вес полного заряда.
Q – вес средний снаряда  .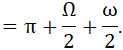
ω – вес газа, остающегося в камере сгорания к концу сгорания.
С – вес газа, изверженного из снаряда к концу сгорания.
с = C/q – коэффициент заряда, соответствующего сгоранию.
E – скорость газообразования вещества.
W – линейная скорость горения вещества.
A – площадь нормального сечения канала орудия.
Sm – сечения отверстия, через которое выходят газы.
P – давление внутри камеры сгорания (в снаряде).
р – давление внешнее.
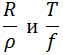 – соответственно постоянная газа, температура сгорания, плотность газа внутри камеры, сила взрывчатого вещества.
u – скорость извержения газа из отверстия.
v – скорость движения снаряда.
q – секундный расход заряда.
γ – показатель политропы.
На черт. 151а изображен реактивный снаряд, составляющий предмет настоящего изучения. Буквы обозначают: a – камеру сгорания, d – сопло B – головку с зарядом.
с) Фазы действия.
Как и в обыкновенной пушке, выталкивание снаряда происходит благодаря сгоранию взрывчатого вещества и образованию и истечению газов, которые повышают давление внутри камеры. Скорость газообразования (вес газа, развиваемого в единицу времени), зависит от формы порохового зерна и от давления. При равных давлениях скорость газообразования будет постоянной, если заряд будет состоять из тонких пластинок, или спиралей, или трубок, или колец. При таких условиях весьма вероятно, что имеет место постоянство отношения между расходом газа q через сопло и весом газа, образуемым в единицу времени топливом при постоянном давлении.
Явление можно разделить на три фазы:
1. Начальная фаза: давление внутри камеры изменяется от р до P.
2. Фаза сгорания при постоянном давлении P.
3. Фаза расширения, в течение которой давление изменяется от P до p.
Эти фазы изображены на черт. 151в.
Очевидно, что при большой плотности заряжения 1-я фаза будет весьма краткой, а 3-я — хотя и продолжительна, но по эффекту действия слабее по сравнению со 2-й фазой. Поэтому займемся сначала исследованием второй фазы, как будто она только одна и имеет место. При этом начальная скорость снаряда получится несколько меньше действительной. При этом мы принимаем числовые коэффициенты соответствующие действительному процессу сгорания и расширения, что подтверждается произведенными опытами. Расчет 3-й фазы будет дан в кратких чертах позднее. Что же касается 1-й фазы, то она соответствует такому же периоду метании обыкновенного снаряда и здесь нет основании предполагать выигрыша энергии.
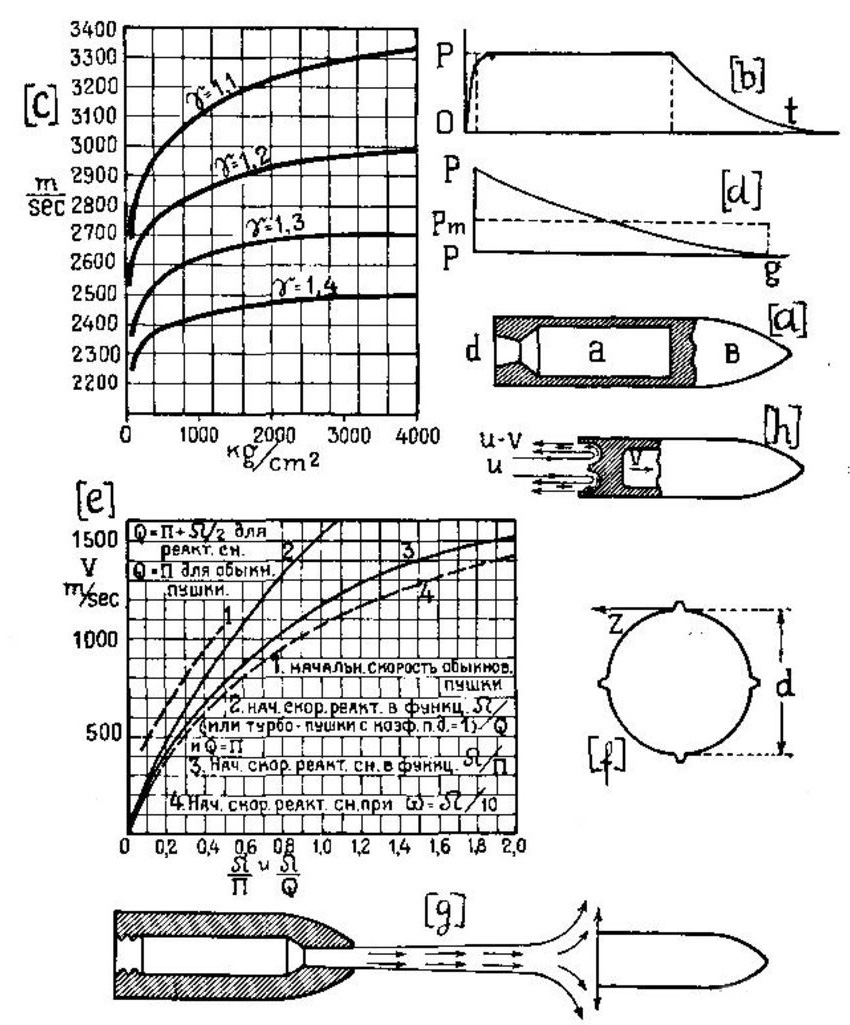
Черт. 151. К теории Д. Пенья. |
|
d) Расчет секундного расхода газа через сопло.
Расход q газа через сопло остается во 2-й фазе постоянным, так как при этом остаются постоянными: внутренней давление P, внешнее – ρ, скорость истечения и плотность газа.
Так как внутреннее давление P выше внешнего, и равно последнему, умноженному на величину 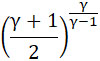 то мы применим формулы истечения газа, в которых знак m соответствует минимальному сечению сопла.
| |
|
 |
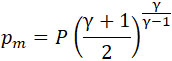(1) |
| |
|
 |
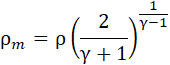(2) |
| |
|
 |
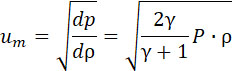(3) |
| |
|
 |
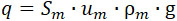(4) |
Из этих формул получаем:
| |
|
 |
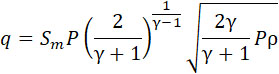(5) |
Так как
| |
|
 |
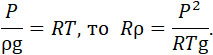(6) |
Подставляя в (5), получим:
| |
|
 |
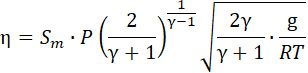(7) |
Допуская, согласно Малляру и Ле-Шателье, что удельная теплоемкость газа не зависит от давления, можно принять температуру Т сгорания постоянной для любого взрывчатого вещества. Поэтому:
| |
|
 |
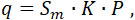(8) |
где
| |
|
 |
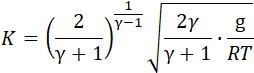(9) |
Для балистита: R = 30,7; Т = 3281.
Для значений γ от 1,1 до 1,4 получим соответственно K изменяющиеся по линейному закону от 0,00622 до 0,00677. Так как K изменяется незначительно, то принимаем его среднее значение 0,0065, и тогда
| |
|
 |
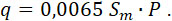(8 bis) |
Положим: Sm = 1; P = 1; тогда q = 0,0065.
Если Sm = 0,0001; P = 10000, то q = 0,0065.
Формула 8bis принята при единицах мер cm и kg. При этом через каждый cm2 проходит 6,5 граммов газа в секунду.
Сила взрывчатого вещества:
| |
|
 |
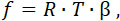(10) |
где β – вес газа, развиваемого 1 kg вещества.
Положим для балистита β = 1. Тогда из (9):
| |
|
 |
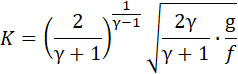(11) |
и
 |
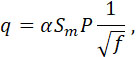(12) |
где  .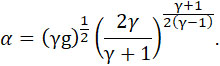
f выражается в kg/m и означает давление, производимое 1 kg взрывчатого вещества, сгорающего в неизменном объеме 1 m3.
Для балистита f = 100840 kg/m. Величины f других взрывчатых веществ можно получить, умножая на 10 величины, данные Бианки в его теории взрывчатых веществ, у которого они выражают давления на cm2 при взрыве 1 kg вещества в неизменном объеме 1 cm3.
е) Расчет реактивного действия во время 2-й фазы.
Если u – скорость истечения газов из сопла, r – реакция газа, то –
| |
|
 |
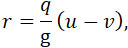(13) |
здесь q = const = 0,0065 SP, и u – также постоянна и определяется формулой (14), характеризующей истечение совершенных газов; когда:
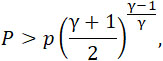
то
 |
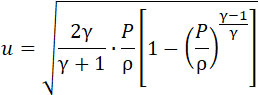(14) |
Так как – P/ρ gRT = gf и T = 3281, то формула (14) получает вид:
| |
|
 |
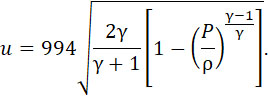(15) |
Принимая для γ последовательные значения до 1,41 и вычисляя для Р = от 4000 до 100 kg на cm2, получим значения и. изображенные на черт. 151с. График показывает, что, при равенстве давлений Р, скорость и тем меньше, чем больше γ.
При γ = 1 (изотермическое расширение газа), конечная кинетическая энергия будет больше таковой же при адиабатическом расширении.
Разность между этими двумя количествами соответствует тепловой энергии, поглощаемой газом для поддержания постоянной его температуры во время расширения.
Большинство авторов, занимающихся исследованием вопросов внутренней баллистики, принимают γ = 1,1 до 1,2.
Однако, отсутствие конечных данных не обязывает нас принимать эти значения при расширении газа, процесс которого в нашем случае несколько отличается от обычной стрельбы.
Явления, происходящие в обоих случаях, вообще говоря, различны. Кроме того, при реактивном снаряде, газ соприкасается со стенками сопла в продолжение всего лишь нескольких десятитысячных долей секунды, тогда как в обычной пушке это соприкосновение происходит в продолжении всего времени движения снаряда в стволе орудия. Поэтому возможно предположить, что в нашем случае γ больше и равно 1,41. Кроме того масса металла орудия, поглощающая тепло, в нашем случае раз в 100 меньше.
При таких условиях получим значение u меньше действительного, и при γ = 1,4 и Р = 1000 kg/cm2, и = 2430 m/sec; при γ = 1,1 и P = 1000 kg/cm2 u = 3100 m/sec.
Черт. 151с показывает, что при данном γ скорость мало изменяется с изменением давления. Поэтому мы можем принять в каждом случае среднее значение u по черт. 151с.
f) Определение начальной скорости снаряда.
Скорость полета снаряда в момент t рассматриваемой фазы, считая от начала этой фазы, практически совпадающего с началом горения, будет
| |
|
 |
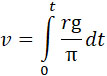(16) |
где π – вес снаряда плюс вес заряда, оставшегося в камере сгорания к моменту t. Поставляя это значение v в формулу (13), получим:
| |
|
 |
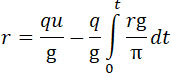(17) |
Имея в виду, что в продолжение этой фазы при постоянном давлении и u – постоянно, получим из (17) при дифференцировании:
| |
|
 |
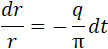(19) |
Обозначим через τ – продолжительность этой фазы; вес снаряда в промежуток времени от 0 до τ – будет изменяться от π + Ω до π + ω, по линейному закону.
При интегрировании уравнения (19), можно вместо переменного значения π подставить его среднее значение Q. Тогда получим:
| |
|
 |
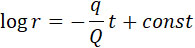(20) |
| |
|
 |
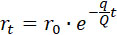(21) |
Но при t = 0, r0 = qu/g (из 13). Поэтому:
| |
|
 |
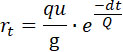(22) |
В этой формуле qt представляет часть заряда, сгоревшего к моменту t. Подставляя это значение r (16), имеем:
| |
|
 |
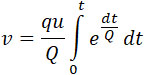(23) |
и по интегрировании:
| |
|
 |
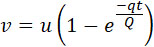(24) |
Из этой формулы следует, что скорость снаряда в конце второй фазы, а также и энергия в конце интервала τ, зависит лишь от скорости истечения газа через сопло, т. е. от давления внутри камеры сгорания и от отношения веса сгоревшей части заряда за интервал τ к среднему весу снаряда.
Определение пути, пройденного снарядом за 2-ю фазу.
Искомый путь:
 |
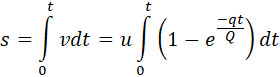(25) |
Интегрируя, имеем:
 |
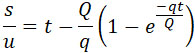(26) |
| |
|
 |
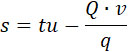(27) |
Для момента t = τ имеем:
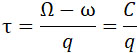
и тогда –
 |
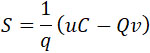(28) |
Отношение C/Q обозначим через c и назовем коэффициентом действующего заряда. При этом предыдущие формулы примут более простой вид:
| |
|
 |
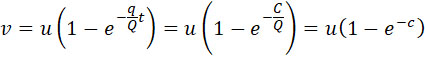(29) |
| |
|
 |
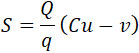(30) |
т. е. путь, пройденный снарядом, прямо пропорционален среднему весу снаряда и обратно пропорционален секундному расходу горючего; при этом принимается, что С и v постоянны до конца 2-фазы.
Так как мы пока условились пренебрегать баллистическими процессами первой и третьей фаз, то формулы (29) и (30) дают нам начальную скорость и путь проходимый снарядом в канале открытой пушки или соответственную полезную длину самой пушки.
|
