|
с) О сопротивлении жидкостей и о реакции при их извержении.
Д. Рябушинский в своей статье «Sur la resistance des fluides et la reaction d’une jet», опубликованной в «Revue général de l’aéronautique» Numero 6, 1925 г., a также в книге «Ill congrés international de la Navigation aérienne». Tome II, pg. 180, излагает теорию сопротивления жидкостей при разных скоростях и приводит результаты своих опытов, произведенных в связи с упомянутым вопросом, при полете ракет. В этом отношении эта работа является как бы продолжением его предыдущей работы «Теория ракет».
Ниже нами приводится изложение первой части его работы (сопротивление жидкостей) лишь постолько, посколько это необходимо для понимания интересующей нас второй части (реакция жидкостей при их извержении). Перевод этой последней части мы даем полностью 1).
1. О сопротивлении жидкостей.
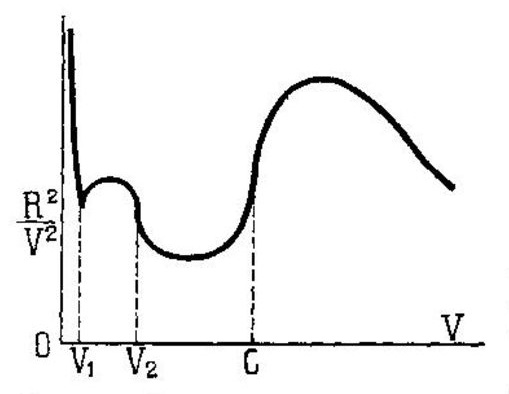
Черт. 145. Кривая сопротивления воздуха. |
|
Если тела движутся равномерно прямолинейно или вращательно, в безграничной жидкости, то кривые выражающие зависимость отношения R/V2 (сопротивления к квадрату скорости) от скорости зависят от формы и размеров тел и от свойств жидкости. Однако, общий вид этих кривых, характеризуемых некоторым количеством их особенных точек, остается, вообще говоря одинаковым; на черт. 145 изображена схематически подобная кривая.
В некоторых случаях критические скорости V1 и V2 могут совпападать. В части, соответствующей скоростям, меньшим V1, движение неразрывно и анализ его дает точное решение при помощи интегрирования уравнений Навье.
Опыты в этом случае согласуются с теорией. Далее же скорости V1 режим истечения и закон сопротивления резко меняются, что можно объяснить возникновением вихрей благодаря трению жидкости о тело и распространяющихся в поток. Следующей особенной точкой кривой, является точка V2, которой соответствует новое изменение режима, при чем, в известных случаях, это изменение может быть довольно резким. Это явление связано с разрывом струй жидкости.
1) Подобный прием был произведен в Италии, где изложение этой работы Д. Р. было дано в «Notiziario technico di Aéronautica», 1927, № 8, pg. 1.
Третией особенной точкой кривой, является точка C, соответствующая скорости жидкости, равной скорости звука. При этом происходит резкое увеличение коэффициента сопротивления.
После опытов и фотографий Маха был сделан ряд попыток связать теорию сопротивления при больших скоростях с теорией волн ударов Римана, Ранкина и Гюгонио. Главнейшие исследования в этом напралении были сделаны Себертом, Гюгонио, Виеллем, Гадамаром и Рэйлеем. (См. Гидронамику Ламба. 1924 г.).
Рэйлей основывается на теории Ранкина, дополняя ее учетом трения, чтобы определить изменение, которому подвергается постоянная формула Лапласа pvγ, при переходе волны удара. При этом он получает отношение P2 / P0 давления в критической точке при нулевой точке при нулевой скорости к давлению в жидкости безвихревой в виде:
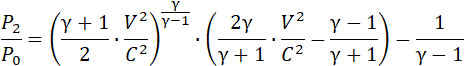 |
(1) |
откуда
| |
|
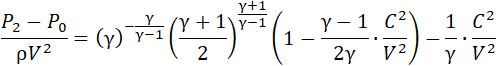 |
(2) |
Ламб дает несколько значений, вычисленных по этой формуле.
| |
|
|
|
|
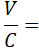 |
1 |
2 |
3 |
4 |
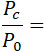 |
1,90 |
4,19 |
11,7 |
20,6 |
и замечает, что опыты Стантона, произведенные со скоростями в 2 – 3 раза большими скорости звука, хорошо согласуются с этой теорией. Следует однако заметить, что формула (1) является не вполне строгой и окончательной, так как она основывается на некоторых гипотезах, которые Ранкин и Рэйлей должны были принять, так как трудно дать полный баланс температурных изменений, происходящих в критической зоне АВ (черт. 144 d).
2. Реакция жидкостей при их извержении.
Ниже я излагаю теорию задачи о давлении при критической точке от нулевой скорости до скоростей, превосходящих скорость звука, основываясь на теореме количества движений.
Предположим, что газ вытекает из резервуара А (черт. 146 a и B), настолько большого, что движение можно считать постоянным. Дюза может быть или не быть, при чем сечение ее сначала суживающееся, а потом расширяющееся. Вследствие этого отношения давлений внутреннего к наружному
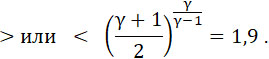
Допустим далее, что угол расширения внешней части дюзы настолько мал, что можно принять скорости в ней параллельными ее оси, и что длина дюзы (конуса) настолько велика, что получается полное расширение.
Давление в сечении S' (черт. В) поэтому будет равно внешнему давлению Pa как в сечении (черт. а), каковой буквой мы обозначаем в случае 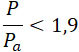 – площадь выходного отверстия в тонкой стенке резервуара А, а в случае – площадь выходного отверстия в тонкой стенке резервуара А, а в случае 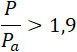 – площадь сечения, где в дюзе равнодействующая гидродинамических давлений ровна нулю. – площадь сечения, где в дюзе равнодействующая гидродинамических давлений ровна нулю.
На основании поставленных условий и теоремы проекций количества движений можно написать:
| |
|
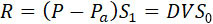 |
(3) |
Здесь D – выражает массу, которая протекает в единицу времени через единицу виртуальной площади S0 (суммы минимальных сечений элементарных струй) извержения, Т – окончательная скорость извержения, определяемая по формуле Сен-Венана:
| |
|
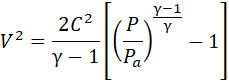 |
(4) |
Здесь С – скорость звука при внешних давлении и плотности.
Расход D – равен (ρa V] или (ρ0 С0), в соответствии с 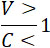 . .
Плотность ρ0 и скорость V0 связаны с плотностью ρ и давлением P снаружи резервуара отношением:
| |
|
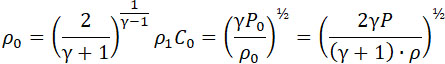 |
(5) |
Принимая во внимание формулы (4) и (5), получаем из (3)
| |
|
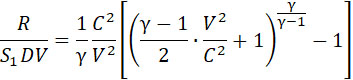 |
(6) |
или:
| |
|
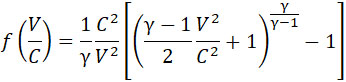 |
(7) |
если 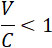 и и
| |
|
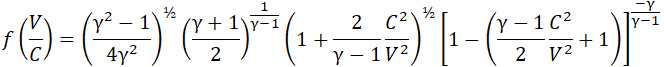 |
(8) |
если 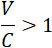
Вид кривой 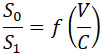 представлен на черт. 146с). представлен на черт. 146с).
Вводя сечения S и S', определяемые равенствами:
| |
|
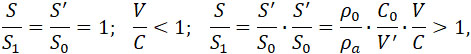 |
(9) |
можно формулы (6) представить в виде:
| |
|
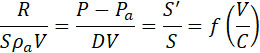 |
(10) |
Значение этой последней подстановки следующее:
Когда (V : C) < 1, давление в сжатом сечении S0 (черт. 146а) равно внешнему давлению Ρa, но когда (V : С) > 1 (черт. 146B) оно равно
| |
|
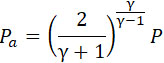 |
(11) |
и струя должна еще расширяться, пока давление не упадет до Pa
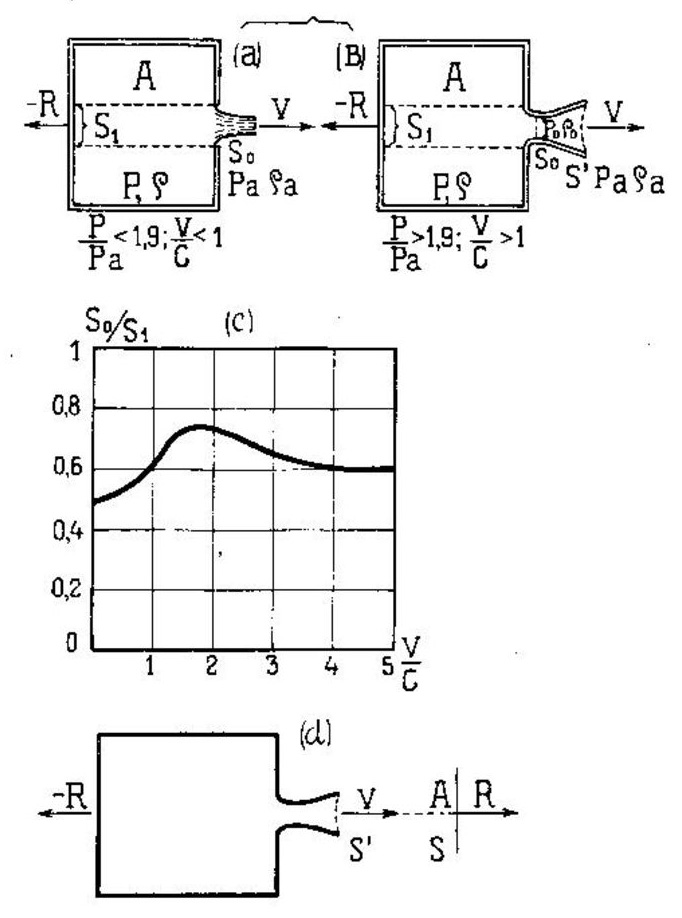
Черт. 146. К теории Рябушинского. |
|
Обозначим, как это вытекает из формул (9), через S' – площадь сечения, соответствующую такому расширению (черт. 146 B), и через S – площадь сечения, определяемого равенством:
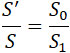 |
(12) |
Вводя сечение S1, мы получим величину реакции R независимо от того, будут ли скорости V больше или меньше скорости звука при внешней плотности ρa; Sρa V выражает массу жидкости, вытекающей в единицу времени из резервуара A, если нет сжатия струи, т. е. если на основании (12) и на основании определении сечения S1:
| |
|
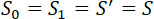 |
(13) |
Полагая в формуле (7) V = 0, получим f(0) = ½. Если жидкость не сжимаема, то в формулах (7) и (8) следует принять С = ∞ и тогда f(V/C) = ½, для некоторой определенной скорости V. Можно предположить, что в этом предельном случае истечение определяется не упругостью жидкости, но, например, движением поршня в резервуаре A.
Реакцию R можно представить суммою двух членов:
| |
|
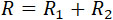 |
(14) |
из них первый:
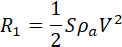 |
(15) |
зависит лишь от инерции, а второй:
| |
|
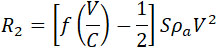 |
(16) |
выражает увеличение реакции благодаря сжимаемости жидкости.
Предположим, что перед струей жидкости помещена плоскость сечения S перпендикулярно к оси симметрии извергаемой струя.
В проблеме сопротивления среды движению тел, которая является к как бы обратной таковой же при реакции извержения жидкости, миделевое сечение тела S соответствует относительному давлению в условиях (13) при безвихревом движении.
Если поток, встречая плоскость S (черт. 146 d), совершенно теряет горизонтальную скорость, до давление R на нее, на основании теоремы о проекциях количеств движения, равно по величине, но обратно по знаку реакции потока на резервуар. Полагая, в этом случае, в уравнении (10)
| |
|
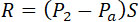 |
(17) |
где P2 – выражает давление на элемент площади S, можно написать
| |
|
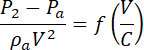 |
(18) |
и
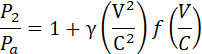 |
(19) |
где 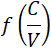 определяется уравнениями (7) и (8). Кривая, выражающая (19), имеет maximum при определяется уравнениями (7) и (8). Кривая, выражающая (19), имеет maximum при
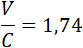 |
(20) |
Уравнение (17) определяет наибольшее сопротивление. В действительности уравнение (18) или (19) определяет давление точно только для точки А симметрии плоскости, где скорость – 0. Если изменить размеры или форму препятствия, о которое ударяется поток, но лишь сохраняя ось симметрии его, совпадающей с таковой же потока, то полное давление потока на препятствие более или менее изменится, но давление в точке A нулевой скорости все же выражается уравнениями (18) или (19). Если отношение (V:C) < 1, то давление, определяемое по уравнению (19), одинаково с тем, которое дает формула Сен-Венана; но если (V:C) > 1, то получается расхождение.
Закон адиабаты не может быть непосредственно более применен. И это указывает на необходимость введения волны удара (une onde de choc).
Некоторые значения отношения P2 и Pa определенные по формуле (9) приведены ниже; их можно сравнить с теми, которые получены по уравнению (1) Рэйлея:
| |
|
|
|
|
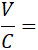 |
1 |
2 |
3 |
4 |
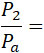 |
1,90 |
5,03 |
9,45 |
15,03 |
Допуская некоторые упрощающие гипотезы, можно применить изложенную теорию к приближенному определению полного сопротивления тел 1).
В заключение приводим описание некоторых опытов, произведенных нами для изучения реакции истечения газов при взрыве пороха в пушке открытой с обоих концов и в ракетах. Сначала выведем несколько формул, хотя и приближенных, но все же дающих характеристику работы этих пушек и ракет.
Обозначим через: m – массу взрывчатого вещества: (горючего), ρ – его потенциал, g – ускорение силы тяжести, u – виртуальную скорость истечения газа, M – массу тела, бросаемую со скоростью V благодаря реакции газа. Применяя законы сохранения количества движения центра тяжести и сохранения энергии, получим в первом приближении:
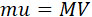 |
(1) |
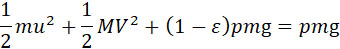 |
(2) |
Член (1 – ε) pmg выражает часть энергии горючего, теряемой бесполезной работы. Коэффициент полезного действия – будет:
| |
|
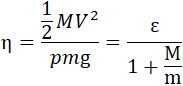 |
(3) |
Полагая, что ракета брошена под углом 45°, и пренебрегая влиянием сопротивления воздуха, получим наибольшую дальность полета ее.
| |
|
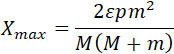 |
(4) |
Если m сравнительно мало по сравнению с M, и коэффициент ε постоянен, то наибольшая дальность полета пропорциональна квадрату веса употребленного горючего и обратно пропорциональна квадрату веса снаряда. Большая часть бросаемого веса относится к весу оболочки ракеты. Поэтому является, пожалуй, выгодным, чтобы оболочка ракеты оставалась бы на месте и выбрасывался бы только снаряд. В результате мы и получаем пушку, открытую с обоих концов.
1) Mémoral de l’Artillerie Française. Fase. III. 1923. p. 710.
Из формулы (3) видно, что коэффициент полезного действия повышается при уменьшении М : m, поэтому упомянутая пушка получает преимущество для случая ракет и пушек большой мощности, лишь бы коэффициент ε не был слишком мал.
Рассмотрим теперь применение ракеты в качестве бабы при забивки свай. В этом случае оболочке ракеты можно дать форму цилиндра, открытого с обоих концов, и одеваемого на голову сваи. Реакция газа при взрыве патрона заставляет сваю углубляться в землю.
Обозначим через M – массу свай, V – скорость ее погружения.
R – сопротивление грунта (постоянное в первом приближении) е и t – глубина и продолжительность забивки сваи. Остальные буквы имеют то же значение, что и раньше,
Формулы (1), (2), (3) применяются и в этом случае, но к ним можно прибавить еще две, которые выводятся на основании закона импульса и теоремы живых сил:
| |
|
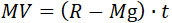 |
(5) |
| |
|
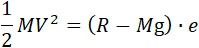 |
(6) |
из (5), (6) и (3) получаем:
| |
|
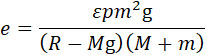 |
(7) |
| |
|
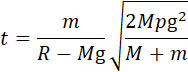 |
(8) |
Если m мало по сравнению c М и ε – не изменяется, то погружение сваи пропорционально квадрату веса горючего. Обозначая через S сечение сваи и через b среднее сопротивление грунта, можно заменить в этих формулах R через bS.
Рассмотрим два численных примера. Пусть вес сваи Mg = 200 kg, Вес горючего mg = 20 kg, потенциал горючего р – 300000 т, сечение сваи – 100 cm2; сопротивление b = 100 kg/m2 коэффициент ε = 0,1. Подставляя эти значения и формулы (3), (7), (8) – получим:
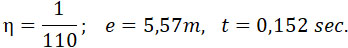
Второй пример. Пусть вес горючего 250 гр., а все остальные величины те же, как и в первом примере:
Тогда
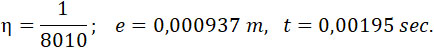
Если мы употребим то же количество горючего, как и в первом примере, т. е. 20 kg, по малым порциям (по 250 g), то после 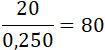 взрывов мы получим глубину погружения 0,000937 + 80 = 0,075 m вместо глубины 5,57 m, полученной при взрыве 20 kg сразу. На практике разница будет вероятно менее значительной, так как сопротивление зависит от V, но все же она останется довольно большой. взрывов мы получим глубину погружения 0,000937 + 80 = 0,075 m вместо глубины 5,57 m, полученной при взрыве 20 kg сразу. На практике разница будет вероятно менее значительной, так как сопротивление зависит от V, но все же она останется довольно большой.
На черт. 147 изображена небольшая пушка, открытая с обоих концов, в том виде, как она была построена в 1916 году в Институте в Кучине. Длина стальной трубы ее была 1 метр, внутренний диаметр – 7 cm, укреплялась она на легкой подставке. В качестве снарядов служили деревянные цилиндры, вес и устойчивость которых увеличивались прибавкой к их передней части свинца. На черт. 147 виден этот цилиндр, всунутый в жерло пушки. Эти цилиндры выбрасывались взрывом пороха, заключенного в патроны из листового железа. Оболочка этих патронов выбрасывалась не сильно и разорванной и сильно деформированной падала на землю. Цилиндры же выбрасывались реакцией газа, без содействия инерции особой массы, как это имеет место в пушке Дэвиса 1).
Вес пушки, считая и подставку – 7 kg, вес снарядов – 3 и 4 kg. Вес зарядов – соответственно 300 и 400 g. Порох был черный. Дальность выстрела в среднем 320 m. Отдача равнялась нулю. Пушка даже не имела склонности ни падать ни наклоняться после выстрела. Этот результат тем более замечателен, что вес снаряда был иногда более половины веса пушки.

Черт. 147. Ракета в пушке. |
|
Дальнейшие опыты в этом направлении производились нами на пляже вблизи Биаррица в 1924 г.
На черт. 148 вверху изображена ракета с боковыми отверстиями. Реакция вырывающегося из них газа производит сильное вращение ракеты вокруг ее оси. Полет таких ракет напоминает полет снарядов из нарезных орудий.
На черт. 149 изображена ракета на треноге (от фотоаппарата). Дальности полета подобны проведенным выше. На черт. 150 показана установка для забивки свай. Длина сваи была 195 cm, часть ее, всунутая в стальной цилиндр, была длиною 50 cm. Диаметр сваи внутри цилиндра – 8,8 cm, а снаружи его – 10,5 cm. Внутренний диаметр цилиндра – 9,3 cm. Вес сваи — 12,9 kg. Вес заряда – 575 g. Глубина погружения сваи в песок – 60 cm **).
1) «La Nature», 2 decembre. 1916.
**) Опыты с применением динамита при забивке сваи были произведены еще в 1881 году в Буда-Пеште, лейтенантом – полковником Prodanovac (Paul Chalon «Les explosifs modernes», p. 691). Веса зарядов были по сравнению с весом свай весьма малы, и заряд прикрывался песком или глиной.

Черт. 148. Ракеты Рябушинского. |
|
На черт. 148 снизу изображена ракета, укрепленная на диске, с боковыми каналами благодаря которым вся система могла вращаться вокруг оси | диску. Вес всей системы – 533 g. Она бросалась примерно под углом 25° при заряде весом 50 g и падала, пролетев 110 метров, при чем при падении делала несколько рикошетов на мокром песке пляжа.
Успех работы этих ракет зависит от сопротивления патрона с зарядом. Необходимо чтобы взрыв происходил быстрее, чем выход газов из устья оболочки ракеты.
Интересно отметить, что если применять патроны из бумаги, то при добавлении к их толщине нескольких листов, ракета, вместо того, чтобы падать у места выстрела, пролетала сотни метров.

Черт. 149. Ракета на треноге. |
|

Черт. 150. Реактивный копер |
* * *
|