|
6. Экспериментальная проверка полученных формул.
Для определения импульса опытным путем, я подвешивал ракеты к баллистическому маятнику, отмечал отклонения его, измеряя дальность полета ракеты в свободном полете и получал некоторые кривые давлений при помощи динамометра.
Баллистический маятник не вполне отвечал моим исследованиям, так как импульс, сообщаемый истечением газов из ракеты, не мгновенен; маятник уже отклоняется на значительный угол, а газ еще продолжает истекать.
Это обстоятельство значительно усложняет подсчеты, которые необходимо произвести для определения импульса I.
Чтобы ослабить это неудобство, я предпринял в Институте постройку большого баллистического колеса, 4 m диаметром. Это колесо состояло из рычага, расположенного симметрично относительно оси, вокруг которой он мог вращаться. Ракета прикреплялась к одному (или к обоим) концу этого рычага.
Ось при помощи шариковых подшипников опиралась на две массивные колонны, установленные на кирпичном фундаменте.
Момент инерции этого колеса был настолько велик, что можно было пренебрегать его изменением, обязанным истечению газа.
Скорость и угловое ускорение баллистического колеса могли измеряться хронографом. Таким образом имелись все необходимые элементы для определения реакции и импульса ракет 1).
Я сожалею, что не имел возможности окончить постройку этого аппарата и применить его к изучению ракет 2).
Три первых метода, упомянутых в начале этого параграфа, дают удовлетворительное подтверждение изложенной выше теории.
7. Влияние дополнительного взрыва.
Рассмотрим теперь случай, как это делает Поморцев, когда в ракете помещается бензин или эфир, которые образуют с сжатым воздухом взрывчатую смесь, или порох, или какое-нибудь иное взрывчатое вещество.
1) Я уже применял аналогичный метод (измерение условных ускорений) для определения пары, производящей самовращение симметричных поверхностей, и получал результаты, соответствующие теории, несмотря на малую величину самих сил.
Я пробовал в последнее время применить этот метод в лаборатории для изучения ветренных мельниц в Аскове (Дания) к большой мельнице профессора Поль-ля-Кура, но момент инерции этой мельницы был настолько мал по сравнению с парой давления ветра на ее крылья, что малейшие изменения ветра производили в ходе мельницы такие аномалии, которые чрезвычайно усложняли вопрос.
2) Было бы интересно изучить работу двигателей с прямой реакцией, работающих автоматично, подобно бензиновому двигателю.
Для определения импульса I в этом случае, нужно применить формулу (11), или, если приблизительно γ = 1,4, формулу (26).
Последнюю можно изобразить в виде:
| |
|
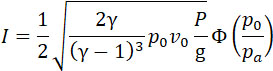 |
(28) |
Легко вычислить v0 и, если известна реакция взрыва, то и абсолютную температуру Т и давление p0. Я считаю, что можно с удобством заменить сжатый воздух порохом. Тогда конструкция ракеты значительно упрощается, так как достаточно положить внутрь ее некоторое количество пороха и плотно закрыть отверстие.
8. Определение дальности полета ракеты.
Обозначим через M – массу ракеты, через m – массу газа, которую она содержит в момент t, и через ω – скорость полета ракеты.
Тогда можно написать:
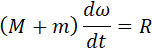
откуда
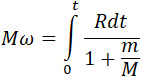 |
(29) |
Принимая во внимание формулы (1) и (12), находим:
| |
|
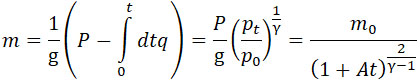 |
(30) |
Подставляя это значение в формулу (29), получаем:
| |
|
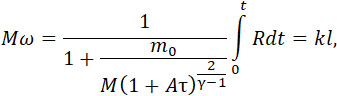 |
(31) |
где τ удовлетворяет условию 0 < τ < t.
Член – 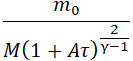 представляет собою вообще малую дробь, и потому коэффициент k мало отличается от единицы. представляет собою вообще малую дробь, и потому коэффициент k мало отличается от единицы.
Так как продолжительность t истечения сжатого газа мала по сравнению с полным временем полета ракеты, то можно определить дальность полета ракеты Xmax , полагая, что ракета брошена под углом 45º. Пренебрегая сопротивлением воздуха, получаем:
| |
|
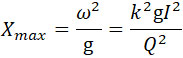 |
(32) |
где Q – вес ракеты.
Заменяя в этой формуле I его выражением (28), получим:
| |
|
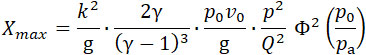 |
(33) |
9. Влияние длины ракеты на дальность полета.
Вес ракеты Q и вес Р сжатого воздуха, находящегося в ней, могут быть выражены в функции l ракеты, именно:
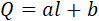
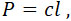
где коэффициенты а, b, с не зависят от l. Подставляя эти значения в формулу (33), находим:
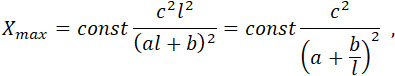
увеличение длины ракеты увеличивает дальность ее полета.
10. Приложение полученных формул к численному примеру.
Рассмотрим ракету, состоящую из стальной трубы длиною l – 2 m и внутреннего диаметра 7 cm. Вес 1 т этой трубы можно принять 5 kg, вес сопла и дна – 2 kg, вес стабилизатора – 0,5 kg. Вес всей системы:
10 + 2 + 0,5 + 5 = 17,5 kg.
Предположим, что ракета наполнена воздухом, сжатым до 400 атмосфер.
Необходимо в формуле (33) положить:
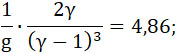
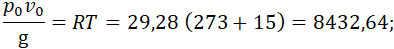
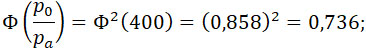
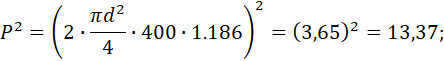
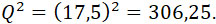
Производя подсчеты и полагая k = 1, находим:
Xmax = 1317 т.
11. Сравнение ракеты с пневматической пушкой.
Обозначим площадь нормального сечения и пневматической пушки (черт. 144а) и таковую же ракеты (черт. 144b) через S; через l0S – начальный объем сжатого воздуха в пушке и в ракете; через l1 полную длину пушки; через M – массу снаряда А, бросаемого пушкой и переносимого ракетой; через M1 – массу ракеты без снаряда, через p0 начальное давление в пушке и в ракете; через р1 – давление в пушке, когда снаряд покидает ее; через m – массу воздуха сжатого в пушке и в ракете.
Для пневматической пушки можно написать:
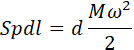
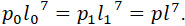
Интегрируя, получаем:
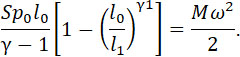
Поэтому, для пневматической пушки:
| |
|
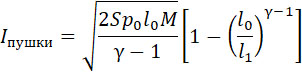 |
(34) |
Полагая в формуле (26) l = l0 и
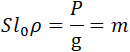
имеем:
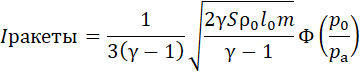
Отношение между дальностью Xпушки, на которую выбрасывается снаряд из пушки и дальностью Xракеты, на которую он (такой же массы) переносится ракетой, равно:
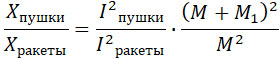
или, заменяя импульсы их выражениями (34) и (35):
| |
|
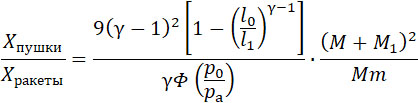 |
(36) |
Рассмотрим частный случай, когда 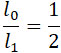 – (черт. 144а), а остальные величины, входящие в (36), те же, которые мы выбрали в примере предыдущего параграфа. – (черт. 144а), а остальные величины, входящие в (36), те же, которые мы выбрали в примере предыдущего параграфа.
Полагая:
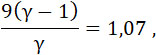
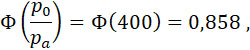
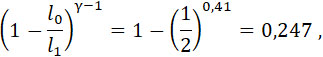
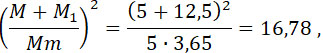
получаем искомое соотношение:
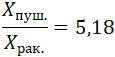
при условии, что сопротивление воздуха в учет не принимается.
При сделанном сравнении, мы предполагали, что в обоих случаях одинаковы лишь полезные веса, т. е. веса снарядов А (черт. 144а). Если же предположить лишь равенство переносимых полных масс, то, заменяя в формуле (36) член 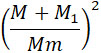 через через 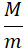 и придавая другим величинам таковые же значения, как в предыдущем примере, получим: и придавая другим величинам таковые же значения, как в предыдущем примере, получим:
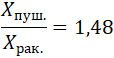
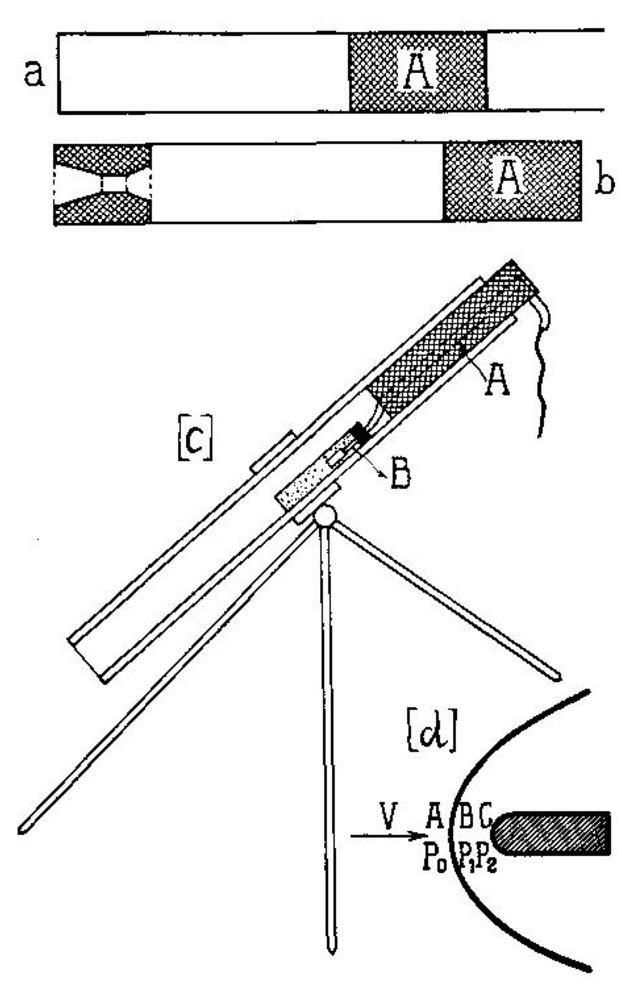
Черт. 144. Ракеты Рябушинского. |
|
12. Реактивная пушка.
Пример, рассмотренный в предыдущем параграфе, показывает, что главная часть веса, переносимого ракетой, падает на самую ракету (а не на снаряд).
Я построил в 1916 г. в Институте небольшую реактивную пушку, которую можно уподобить ракете, оболочка которой остается неподвижной, а полезный груз (снаряд) вылетает один. На черт. 144с дана схема этой пушки. Бомба A выбрасывается взрывом пороха, заключенного в жестяном цилиндре B. Вес пушки – 7 kg, вес снарядов – 3 и 4 kg. Соответственные заряды в 300 и 400 kg черного пороха выбрасывали эти снаряды в среднем на 320 т.
Пушки обычная и реактивная могут рассматриваться как два крайних случая, между которыми находятся пушки без отдачи, бросающие более или менее значительные массы в направлении, обратном полету снаряда.
|