|
Глава V. Работы Д. П. Рябушинского

а) Предисловие.

Черт. 142
Д. П. Рябушинский. |
|
Д. П. Рябушинский (черт. 142) работает в области различных вопросов гидро и аэромеханики, авиации и воздухоплавания с 1904 года, когда им был основан Аэродинамический Институт в Кучино, близ г. Москвы. С 1906 по 1914 г. им было выпущено пять выпусков (бюллетеней) трудов этого Института, в котором большинство работ принадлежит ему самому. Выпуск 6-й появился уже заграницей (Париж – 1920 г.). В этом выпуске Д. Рябушинский поместил оригинальную статью по теории ракет и описывает свои опыты над ракетами и реактивными пушками, произведенные в 1916 году в Кучино, но не опубликованные до сего времени. В виду интереса представляемого этой статьей, мы помещаем ниже ее полный перевод.
b) Теория ракет.
Статья Д. П. Рябушинского, помещенная в выпуске 6-м трудов Аэродинамического Института в Кучино.
1. Пневматическая ракета генерала Поморцева.
Пневматическая ракета генерала Поморцева состоит из стальной трубы (черт. 143а), один конец которой (В) закрыт, а другой (а) имеет сопло (поверхность сходящуюся и расходящуюся). Отверстие (а) закрыто пробкой, которая при помощи остроумного приспособления может быть открыта в любой момент. При опытах, произведенных в Институте, воздух в этой ракете сжимался до 100 – 125 атмосфер, и в нее вводили бензин или эфир, чтобы образовать взрывчатую смесь, или помещали в нее порох. Для метания этих ракет Поморцев снабжал их своими известными стабилизаторами (черт. 143b и 19d) и пользовался станком, который он применял при опытах с обыкновенными ракетами.
Поморцев не мог закончить своих опытов; он скончался в июне 1916 г. от болезни сердца, которой он давно страдал. Он был одним из известных пионеров воздухоплавания в России, автором многочисленных работ по авиации и метеорологии и обладал возвышенной душой, сохранив до самой смерти в своих научных изысканиях юношеский энтузиазм.
По желанию Поморцева я продолжал его изыскания после его смерти. Настоящая работа и является результатом моих работ. Я применяю к расчету ракеты Поморцева известную теорию истечения сжимаемой жидкости из сосуда, при чем давление в нем уменьшается по мере истечения газа.
Опыты в общем подтверждают эту теорию, К сожалению я не могу опубликовать результаты опытов (оставшиеся в Кучино).
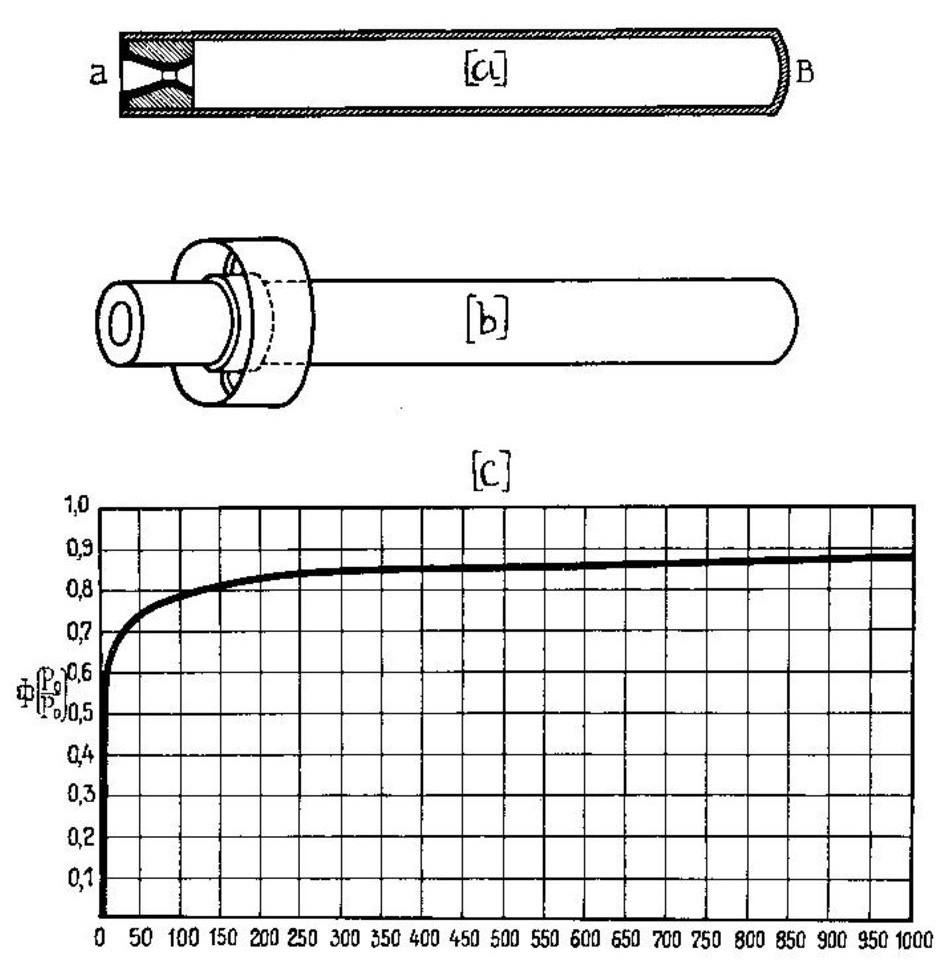
Черт. 143. Ракеты Поморцева. |
|
2. Изменение давления в ракете в функции времени.
Обозначим через Р начальный вес воздуха, сжатого в ракете, через q – вес воздуха, вытекающего через ее отверстие в единицу времени в момент t. Полагая процесс по адиабате, можем написать:
| |
|
 |
(1) |
где St и pt плотность и давление внутри ракеты в момент t, и S0 и p0 те же величины в начальный момент t=o, когда открывается отверстие ракеты.
Обозначим череч Sm – площадь минимального отверстия у выхода из ракеты; um и Sm – соответствующие ей скорость и плотность, и g – ускорение силы тяжести, тогда имеем:
| |
|
 |
(2) |
Согласно теории истечения газов, когда отношение давления pt к внешнему давлению pa удовлетворяет неравенству
| |
|
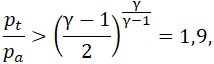 |
(3) |
имеем:
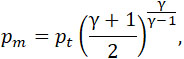 |
(4) |
| |
|
 |
(5) |
| |
|
 |
(6) |
поэтому
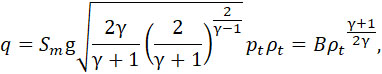 |
(7) |
где
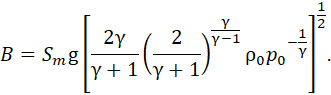 |
(8) |
Подставляя (7) в (1), получаем:

откуда, взяв производную имеем:
| |
|
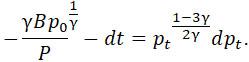 |
(9) |
Интегрируя выражение (9) и имея в виду, что для t = 0 и pt = p0, получим:
| |
|
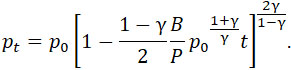 |
(10) |
Заменяя в этой формуле В его аначением (8) и полагая
| |
|
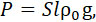 |
(11) |
где S – есть площадь нормального сечения ракеты, l – ее длина, можно написать:
| |
|
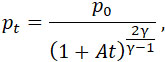 |
(12) |
где, для упрощения, положено:
| |
|
 |
(13) |
Обозначая через t промежуток времени, в течение которого давление внутри ракеты сравняется с давлением pa вне нее, можно написать:
| |
|
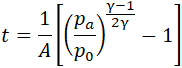 |
(14) |
Исключая А из формул (12) и (14), получим:
| |
|
 |
(15) |
Формулы (14) и 15) выведены в предположении, что расход постоянно определяется выражением (7). В действительности, когда давление pt перестанет удовлетворять условию (3), т. е. когда
| |
|
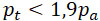 |
(16) |
закон истечения будет иной. Однако, принимая во внимание, что давления, определяемые неравенством (16), сравнительно малы, можно этим обстоятельством пренебречь, так как оно весьма мало влияет на полный импульс, сообщенный ракете, каковой нас в этой работе главным образом и интересует.
При получении этих формул мы должны сделать следующие гипотезы.
1°. В сопле член 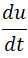 уравнения Эйлера достаточно мал по сравне нию с членами и уравнения Эйлера достаточно мал по сравне нию с членами и 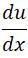 и и 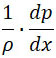 , чтобы его можно было исключить. , чтобы его можно было исключить.
2º. Скорости внутри ракеты весьма малы по сравнению с таковыми же в сопле; поэтому первые считаются, как нулевые.
3º. Давление внутри ракеты в данный момент всюду одинаково.
3. Изменение реакции в функции времени.
Для определения реакции ракеты, следует умножить массу 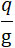 , вытекающую через ее отверстие в секунду, на скорость ua соответствующую разности давления рt – рa . , вытекающую через ее отверстие в секунду, на скорость ua соответствующую разности давления рt – рa .
Эта скорость определяется по формуле Сен-Венана:
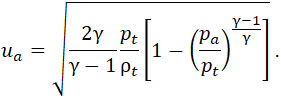
Поэтому:

или, принимая во внимание (12)
| |
|
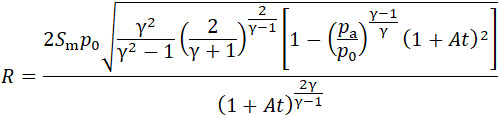 |
(17) |
Полагая в этой формуле t = 0, получим начальную реакцию:
| |
|
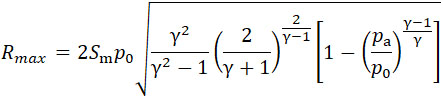 |
(18) |
4. Доказательство теоремы, что импульс, сообщенный ракете, не зависит от площади сечения Sm сопла.
Принимая во внимание формулу (7), получаем выражение для импульса, сообщенного ракете расширением газа:
| |
|
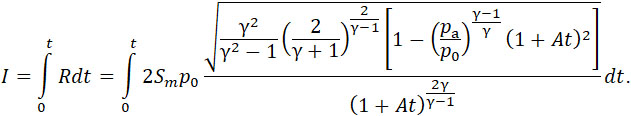 |
(19) |
Докажем, что I не зависит от величины площади Sm сечения сопла. Выражения (13) и (15) позволяют написать:
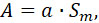
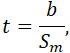
где a и b не зависят от Sm .
Введем новую переменную t1 = Sm • t и преобразуем выражение (19) в следующее:
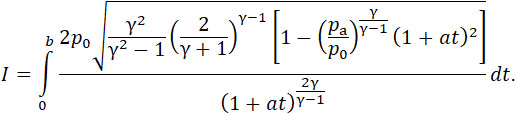
Вторая часть этого выражения не зависит от Sm, а следовательно и I от Sm не зависит, что и требовалось доказать.
5. Определение импульса, сообщенного ракете.
Введем новую переменную
| |
|
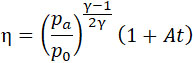 |
(20) |
и преобразуем выражение (19) в следующее:
| |
|
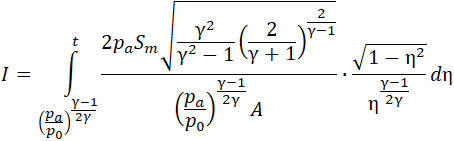 |
(21) |
Если γ = 1,4 то этот интеграл можно выразить в элементарном виде так как тогда 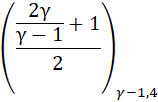 - целое число. - целое число.
Принимая обозначения:
| |
|
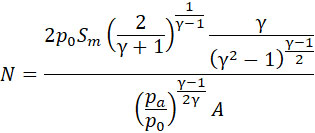 |
(22) |
| |
|
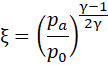 |
(23) |
и полагая γ =1,4, можем написать:
| |
|
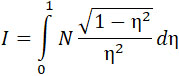 |
(24) |
и полагая:
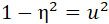 |
(25) |
интегрируем:
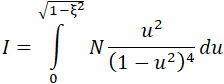
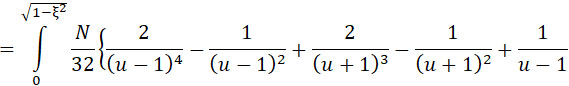
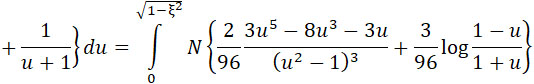

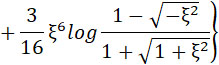
Представим это выражение еще в следующей форме:
| |
|
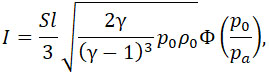 |
(26) |
где
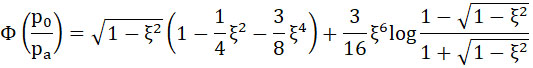 |
(27) |
где ξ выражается формулой (23).
Вид функции (27) изображен на чертеже (143с).
|