|
Глава IV. Элементы теории реактивного двигателя

Теория реактивного двигателя в применении к полету ракет в настоящее время дана в работах Циолковского, Оберта, Годдара, Гоманна и др. и приводится нами в следующих книгах. Здесь же, помимо некоторых теоретических соображений, приведенных уже выше (работы Лорэна и Горохова), приводятся три теоретических справки по этому вопросу: Роста, Држевецкого и Поповатца, каковые отчасти обрисовывают работу двигателя прямой реакции и отчасти (Држевецкий) показывает его родство с другими двигателями летательных аппаратов (геликоптер).
а) Теория Роста.
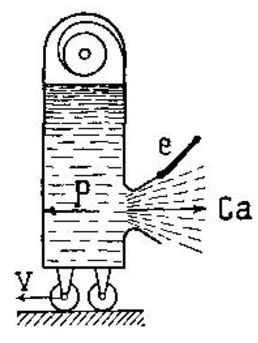
Черт. 140.
К теории Роста. |
|
Представим себе сосуд на колесах (черт. 140), в котором при помощи вентилятора поддерживается постоянное давление воздуха h. Внизу сосуда устроен клапан e. Когда он закрыт, то на его площадь F будет действовать давление Fh. Когда же он будет открыт, то воздух будет вытекать из отверстия со скоростью
| |
ca |
|
= |
√ |
2g |
|
h |
|
= |
|
√ |
2 • 9,81 |
|
h |
|
= |
|
3,961 |
√ |
h |
|
m/sec |
|
|
| γ |
1,296 |
На площадку стенки сосуда, противоположную отверстию, будет действовать то же давление Fh. Кроме того должно действовать в сосуде добавочное давление Fh, которое сообщало бы воздуху скорость Ca. Поэтому на упомянутую стенку будет действовать давление
| |
Р |
|
= |
|
2Fh; но |
|
h |
|
= |
|
v2 γ |
|
, |
|
|
| 2g |
поэтому
| |
Р |
|
= |
|
γ |
|
Fv2 |
|
=~ 0,13 Fv2 . |
|
|
| g |
Если сосуд будет двигаться влево со скоростью v, соответствующей давлению h, то Ca = 0 и сила реакции будет равна статическому давлению Fh или
Если из устья ракеты поперечного сечения F вытекает масса газа со скоростью v m в сек., равная M = 0,13 F•v обладающая энергией
| |
Mv2 |
|
= |
|
0,13 • F • v2 |
|
, |
|
|
| 2 |
2 |
то для получения ее необходимо в двигателе развить
| |
B |
|
= |
|
0,13 • F • v2 |
|
HP , |
|
(1) |
| 2 • 75 • η |
где η – коэффициент полезного действия двигателя.
Сила реакции
| |
P |
|
= |
|
2Mv |
|
= |
|
2 • 0,13 • Fv2 kg |
|
|
|
(2) |
При делении (2) на (1) получаем движущую силу в kg на 1 НР
В 1908 г. в Германии Маврикий Познанский предлагал построить летательный аппарат по этому принципу, при чем сжатый воздух, доставляемый компрессорами, должен был истекать вниз.
Сделаем несколько подсчетов, оценивающих подобный аппарат.
При V = 1 m/sec на 1 HP по формуле (3) и при η = 0,5 придется 75 kg. Однако при этом F =~ 290 m2 или на 100 kg подъемной силы F = 390 m2. При V = 20 m/sec получим на 1 HP P = 3,75 kg и F == 0,036, что дает при Р = 100 kg; F =~ 1 m2.
b) Теория Држевецкого.

Черт. 141. К теории
Држевецкого. |
|
Предположим, что требуется поддержать в пространстве аппарат весом P kg (черт. 141).
Пусть для этого из аппарата отбрасывается газ (или воздух) со скоростью v m/sec. Пусть плотность воздуха 1,29 kg. Для поддержания аппарата в пространстве необходимо, чтобы реакция, возникающая благодаря выбрасыванию газа, равнялась весу аппарата P, т. е.
Так как количество движения равно импульсу силы, то
где M – есть масса выброшенных газов в секунду.
Объем этой массы будет
| |
W |
|
= |
|
m • g |
|
|
|
= |
|
|
M • 9,81 |
|
=~ |
|
8M , |
|
| 1,29 |
1,29 |
Но из (2):
поэтому
Площадь поперечного сечения газовой струи равна
Давление ψ, под которым вырывается газ, определяется из формулы
откуда
| |
ψ |
|
= |
|
( |
v |
) |
2 |
|
в mm вод.столба. |
| 4 |
|
Полное давление по всей площади S струи равно
| π |
|
= |
|
ψ • S |
|
= |
|
( |
v |
) |
2 |
8 |
|
P |
|
= |
|
P |
|
kg , |
| 4 |
|
v2 |
2 |
(Слой воды в 1 mm на 1 m2 весит 1 kg).
При скорости v m/sec производимая полезная работа будет:
или в лошадиных силах
Если коэффициент полезного действия винта или иного движителя ρ, то
Рассмотрим разные случаи поддержания:
Геликоптер. Пусть коэффициент полезного действия винта ρ = 0,8. Вес аппарата P = 500 kg. Площадь винтов S = 10 m2. Тогда по формуле (3) : v = 20 m/sec, а по формуле (5) необходимая мощность равна:
| Tm |
|
= |
|
500 • 20 |
|
= |
|
83 HP . |
| 0,8 • 150 |
Ракета: v = 3000 m/sec.; ρ = 0,5;
| Tm |
|
= |
|
500 • 3000 |
|
= |
|
20000 HP . |
| 0,5 • 150 |
Эту мощность дают взрывчатые вещества, но при малом весе лишь на короткое время.
Примечание: Из формулы (5) следует, что для уменьшения мощности Tm выгодно уменьшать скорость v. Но по формуле (3) при этом увеличивается сильно сечение струи S, что влечет за собою громоздкость и вес аппарата. И лишь практика покажет наивыгоднейшие отношения между S и v.
с) Теория Поповатца.
Предположим, что 1 kg газа имеет при взрыве x атмосфер и расширяется в окружающем воздухе всецело, развивая некоторую живую силу. Пусть t0 – абсолютная температура воздуха и температура после взрыва при постоянном объеме, так что t1 = xt0
Обозначая через Cv удельную теплоту газа при постоянном объеме получим количество тепла, полученного при взрыве 1 kg газа.
cv (t1– t0) .
В конце расширения газ сохраняет температуру t2 t0. Для закрытия цикла необходимо затратить на охлаждение количество тепла
ch (t2– t0) ,
где Cp – удельная теплота того же газа при постоянном давлении. В полезную работу превращается таким образом
cv (t1– t0) – cp (t2– t0) единица тепла.
Обозначая механический эквивалент тепла через E, имеем полученную энергию
| L |
|
= |
|
E cv t0 |
|
[ |
t1 |
|
– |
|
1 |
|
– |
|
cp |
|
( |
t2 |
|
– |
|
1 |
) |
] |
|
кг/мт . |
| t0 |
cv |
t0 |
Допуская, без особой погрешности, расширение по адиабате, т. е. имея
где R – постоянная, получим:
Здесь L – работа, необходимая для сообщения частицам газа, весящего 1 kg скорости истечения, которая, вообще говоря, для разных частиц разная.
Обозначая их среднюю скорость через v имеем:
где g – ускорение силы тяжести. Тогда имеем:
Сделаем численный пример: g = 9,81; R = 29,3; t0 = 290; γ = 1,4.
1) Если v = 250 m/sec, то x = 2,24. Отдача двигателя будет:
и это даже без учета потерь на нагревание стенок двигателя.
2) Если v = 1000 m/sec, то x = 8 atm, и ρ = 0,33.
В общем реактивный двигатель в обычных условиях полета является более расточительным, чем пропеллерный. Однако, он имеет преимущества в весе, объеме и при больших скоростях полета.
* * *
|