|
|
|
|
|
|
|
|
||
Я.И. Перельман
Иллюстрации Ю. Д. СКАЛДИНА
|
|
См. также: РАКЕТОСТРОЕНИЕ. Содержание
Яков Перельман был известен советскому читателю как популяризатор науки, в доступной форме излагавший основы современных на то время научных знаний и достижений. Его книга «Занимательная физика» – одно из лучших классических пособий по физике. В 30-е гг. 20-века Яков Исидорович заведовал в ЛенГИРДе отделом пропаганды, член президиума ЛенГИРДа. Совместно с инженером А. Н. Штерном разрабатывал проект первой советской противоградовой ракеты. Переписывался с С.П. Королёвым по вопросам пропаганды космических знаний, одновременно (1932−1936 г.г.) работая в ленинградском отделе издательства ЦК ВЛКСМ «Молодая гвардия» в качестве автора, консультанта и научного редактора. А 1 августа 1934 года в составе группы ленинградских писателей и учёных-популяризаторов встретился с Гербертом Уэллсом, приезжавшим в СССР. Конечно, книга «Ракетой на Луну» не является в полной мере «научным трудом». но благодаря ей выросло несколько поколений будущих ученных и конструкторов. Например, именно прочтение книг Перельмана «Ракетой на Луну» и «Межпланетные путешествия» положило начало увлеченностью космосом Всеволода Ивановича Феодосьева, в последующем заведующего «ракетной» кафедрой М-1 в МВТУ им. Баумана, члена-корреспондента АН СССР. Именно поэтому я и решил включить ее в «Золотую книжную коллекцию» ракетостроения. Из письма С.П. Королёва Я.И. Перельману (первая половина 1932 года): «Вообще, у нас слишком много написано всяких сложных и несложных вещей и расчетов о том, как будет межпланетный корабль приближаться к Луне и что с ним будет происходить в пути и т. д., а вот для кружковца-гирдовца, жаждущего поучиться, поработать, — для него материала абсолютно нет. ... Мне очень хотелось бы знать Ваше мнение по этому вопросу и ту конкретную форму, в какой Вы себе представляете такого типа литературу. На кого она должна быть рассчитана главным образом, темы, размеры и пр. Может быть, и Вы согласились бы принять участие в этой работе и написать кое-что?»
Я.И. Перельман
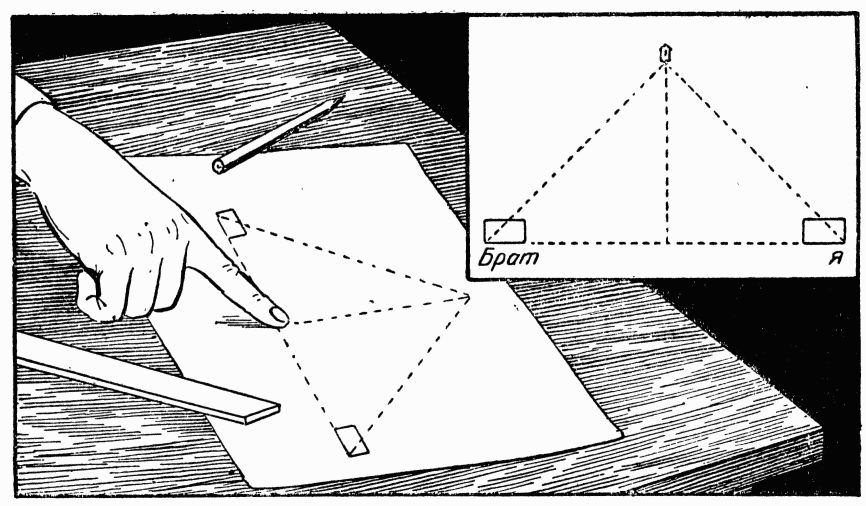
В детстве мне казалось, что если забраться на крышу дома, то до луны будет уже не так далеко. Однажды в лунный вечер я залез на чердак, подошел к слуховому окну и выглянул оттуда. Я думал, что увижу луну вблизи. Куда там! Она висела в небе по- прежнему высоко, словно я смотрел на нее прямо с земли. – Ты собирался, кажется, луну рукой достать? – смеясь, сказал старший брат. – Мне бы на пожарную каланчу забраться, – ответил я. – Другое бы дело было! Не помогла бы и каланча,– сказал брат. – Знал бы ты, как до луны далеко, не трудился бы никуда забираться. – А знают разве люди, как далеко до луны? – Конечно. Расстояние давно измерено. – Значит, люди добирались до луны? – Ну, нет. Там не бывал еще ни один человек. – На луне не были, а расстояние измерили!.. Как же так? – Измерить расстояние до луны можно и не забираясь на нее, а оставаясь на земле. Хочешь, я объясню тебе завтра, как делаются такие измерения? – Наутро брат вышел со мной из дома, прошел несколько улиц нашего маленького города и привел меня к месту, где высоко на березе виднелась скворечница. – Мог бы ты измерить, – спросил он,– на высоте скольких метров висит эта скворечница? – Если влезть на березу, – начал я, – добраться до скворечницы, спустить оттуда веревку. . – Ну, а не влезая на дерево, – перебил меня брат, – стоя здесь, на земле, притом без всякой веревки? Я задумался. Определить высоту скворечницы, не взбираясь на дерево, казалось мне совершенно невозможным. Однако брат взялся это проделать. Вынув из кармана две белые карточки, он дал одну мне и велел отойти в сторону от березы. Сам же, держа в руке вторую карточку, отошел по другую сторону дерева. Приставив карточку к глазу, брат стал на колено, чтобы быть одного роста со мною. Нижний край его карточки был направлен как раз на меня. Закрыв один глаз, он глядел другим на скворечницу так, чтобы взгляд скользил по карточке; в этом направлении он прочертил на карточке прямую линию. Стоя на своем месте, я должен был проделать то же самое. Вы лучше поймете то, что сейчас было сказано, если рассмотрите внимательно нижний правый угол рисунка. Покончив с этим, брат вынул из кармана мерную ленту и промерил расстояние между местами где мы стояли. Оказалось одиннадцать метров. – Готово! – объявил брат. – Можно отправляться домой. – А как же высота? – разочарованно спросил я. – Ведь ты собирался измерить высоту скворечницы. – Для того и идем домой. Там узнаем. Здесь нам больше нечего делать. Это было совсем странно: как можно в своей комнате измерить высоту скворечницы, которая висит где-то за городом? С интересом ждал я, что он станет делать дома.
Брат начал с того, что провел на листе бумаги прямую линию в одиннадцать сантиметров длины. К концам линии он приставил наши карточки, как показано на рисунке (см. ниже). Линии, прочерченные на них, он продолжил на бумаге, пока они не встретились, и измерил расстояние от места встречи до нижней линии. Я не очень-то понимал, зачем все это делается и как отсюда можно будет узнать высоту фонаря. – Вот видишь, – объяснил мне брат, водя пальцем по чертежу,– нижняя линия в одиннадцать сантиметров – это расстояние от моего глаза до твоего, когда мы стояли с тобою у березы. Оно лишь уменьшено: сколько там было метров, столько на чертеже сантиметров. А вот это – направления, под какими мы глядели на скворечницу. Она висит в месте встречи этих линий. Расстояние от нее до нижней линии и есть высота скворечницы, только высота не над самой землей, а над линией наших глаз. Сколько здесь, в этом расстоянии, сантиметров, на столько метров возвышалась скворечница над линией наших глаз. Ведь сантиметр на чертеже соответствует метру на улице. Если к найденной высоте прибавим твой рост, мы узнаем то, что хотели: высоту скворечницы над землей. Понял?
– Это довольно просто. – А понимаешь ты теперь, каким образом могли ученые измерить расстояние до луны, не добираясь до нее? – Конечно: два ученых глядели на луну сразу из двух далеких мест и замечали направления, как мы. – Да, только сделано это было не так легко и просто, как у нас с тобою. Расстояние между обоими учеными было не одиннадцать метров, а несколько тысяч километров; углы же не прочерчивались на картоне, а измерялись точнейшими инструментами. Зато и вывод получился гораздо надежнее. – И что же узнали? Как далеко до луны? – Страшно далеко! Круглым числом четыреста тысяч километров. Ты знаешь, что от Москвы до Ленинграда всего лишь шестьсот сорок километров. До луны же от нас четыреста тысяч километров. Это в шестьсот с лишним раз дальше, чем от Москвы до Ленинграда. Если бы два города на земле были разделены таким большим расстоянием, то знаешь, сколько времени мчался бы поезд от одного к другому? – Целую неделю? – попробовал я угадать. – Сообрази: от Москвы до Ленинграда скорый поезд идет примерно десять часов. Если расстояние в шестьсот раз больше, то и времени уйдет на езду в шестьсот раз больше. Значит, понадобится шесть тысяч часов. Это – двести пятьдесят суток, или восемь месяцев с лишним. Вот как далеко до луны! Ну, что ты скажешь теперь: стоит взбираться на пожарную каланчу, чтобы взглянуть на луну поближе? Я рассмеялся. Брат продолжал: – На свете нет такой высокой башни, с верхушки которой луна казалась бы хоть чуточку ближе, чем с поверхности земли. – А железная башня Эйфеля в. Париже? – спросил я. – Ведь она выше облаков! – Да, случается иной раз, что верхушка ее окутывается облаками. Но ты, вероятно, думаешь, что облака плывут очень высоко? Это неверно: высота их и сравниться не может с высотою луны. Те облака, что окутывают иногда верхушку Эйфелевой башни, находятся не выше трехсот метров. Дождь идет из облаков, плавающих на высоте двух километров, а самые высокие облака, перистые, висят над нами в восьми – десяти километрах. Что все это по сравнению с четырьмястами тысяч километров! Башня Эйфеля имеет в высоту триста метров. Конечно, если бы ты забрался на ее верхушку, тебе показалось бы, что ты страшно высоко над землей. Люди внизу казались бы муравьями. Но будь башня даже втрое выше, она и тогда была бы в четыреста тысяч раз ниже, чем луна над нашей головой. Заметь: непросто в четыреста раз, а в четыреста тысяч раз! Когда вещь делается ближе всего лишь на четырехсоттысячную долю, можно разве это уловить глазами?
– Но если луна тая далека, – спросил я, – то, верно, она и не такая маленькая, как кажется? – Какой же она величины, по-твоему? – Величиной с тарелку, мне казалось. – С тарелку? Ну, хорошо, сегодня вечером мы измерим с тобою, как велика лунная тарелка.
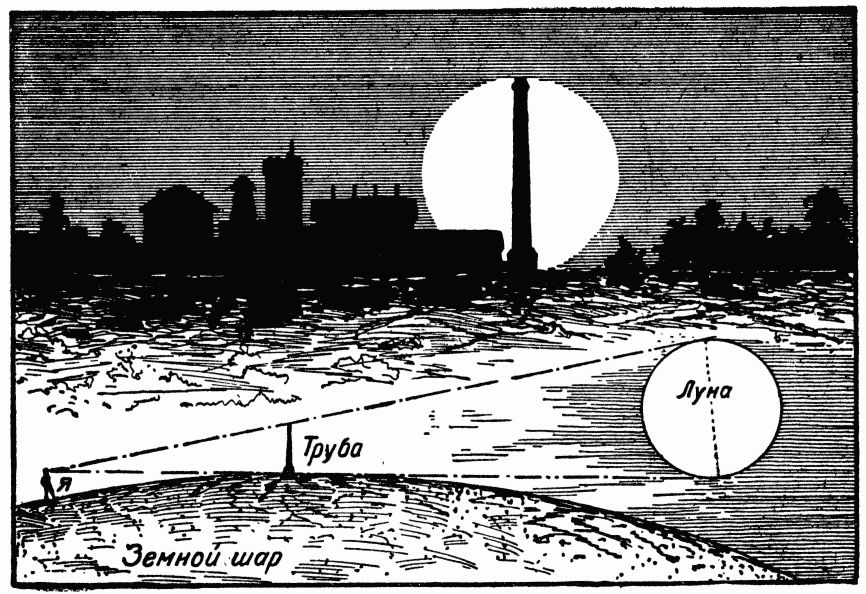
Поздно вечером брат вывел меня за город на ровное, далеко простирающееся поле. Темное небо было безоблачно и начинало заметно светлеть на востоке. – Скоро взойдет полная луна, – сказал брат, указывая на восток, где вырисовывалась на небе черная заводская труба. – Там, позади завода? – Да. И тогда ты поймешь, как могли люди измерить лунный поперечник. Видишь линию, где свод неба как бы сходится с землей? Линия эта называется горизонтом. Ты, конечно, понимаешь, что горизонт – не край земли, а только граница того, что видит глаз. В старину люди думали, что земля плоская, как круглый поднос. Верили, что можно добраться до края этого подноса – туда, где свод неба опирается на землю, и высунуть голову за небесный купол. Теперь даже дети знают уже, что земля никаких границ не имеет, что она круглая не как поднос, а как мяч. Свод неба не существует; нам только кажется, что земля накрыта небесным куполом. – А если дойти до горизонта? – До него дойти никак нельзя. Сколько бы ты ни шел, горизонт все время будет отступать от тебя. Горизонт – это то место, где взгляд наш соскальзывает с выпуклости земного шара и уходит в небесное пространство. На ровном месте взрослый человек видит кругом себя на пять километров; это и есть расстояние до горизонта. Если подняться выше, горизонт отойдет дальше. Для человека маленького роста горизонт ближе.
– А для меня? – Я рассчитал, что при твоем росте ты должен видеть горизонт на расстоянии четырех километров. Завод виден тебе как раз на горизонте – значит от нас до него четыре километра. Если я пригнусь до одной высоты с тобой, то буду видеть завод, как и ты, на самом горизонте... А, вот и край луны показался! – Я не вижу. – Оттого, что ты ниже ростом. Для меня горизонт лежит на километр дальше, и мне видно то, чего ты еще не видишь. Через некоторое время и я увидел верхушку светлого лунного круга, выдвинувшегося из-под горизонта.
Вскоре луна выплыла вся на небо и стала большим медно-желтым кругом за черной заводской трубой. На светлом лице луны труба виднелась очень четко и помещалась как раз между краями лунного круга. – Заводская труба и лунный поперечник кажутся отсюда одной величины, – сказал я. – Вот именно! Для того-то я и привел тебя сюда, чтобы ты это увидел. А как ты думаешь: на самом деле луна и труба тоже одной величины? – Луна дальше – значит, она больше. – Во сколько раз? – Во столько раз больше, во сколько дальше. – Но ты ведь знаешь уже оба расстояния: и до трубы, и до луны. Сообрази же, во сколько раз лунный поперечник больше высоты трубы. Я начал высчитывать вслух: – До трубы четыре километра, до луны четыреста тысяч километров. Луна дальше в сто тысяч раз. Значит, поперечник ее длиннее трубы тоже в сто тысяч раз. – Верно! Теперь скажу тебе высоту трубы. – Откуда ты знаешь? – Сегодня днем я нарочно побывал на заводе и определил там ее высоту. Воткнул в землю отвесно палку и измерил ее тень. Во сколько раз тень палки короче тени трубы, во столько же раз и сама палка ниже самой трубы. – Какой же высоты труба? – Тридцать пять метров. И тогда же я рассчитал, что для тебя она на горизонте должна покрывать поперечник луны. – Теперь я уж сам могу высчитать, как велик лунный поперечник, – подхватил я. – Надо тридцать пять метров умножить на сто тысяч. Сначала умножаю на одну тысячу – получаю тридцать пять тысяч метров, или тридцать пять километров. Эти тридцать пять километров множу на сто – получаю тридцать пять сотен, или три с половиной тысячи километров. – Правильно. Вот мы и узнали длину лунного поперечника: три с половиною тысячи километров. Хороша тарелочка! Я был так поражен этим результатом, что не поверил бы ему, если бы сам не проделал расчета. Так вот какой величины лунный шар! Его поперечник всего в четыре раза меньше земного. – Ты убедился теперь, – сказал брат, – что луна не тарелка, а целый мир. Круг лунного шара шириной с Африку, но полная поверхность луны больше поверхности этого материка. Ученые рассчитали, что полная поверхность лунного шара по обширности лишь немного уступает Азии: в той и другой почти одинаковое число квадратных километров. А Азия, ты знаешь, огромный материк. На нем живет больше половины всего человечества, по нему протекают многоводные реки, проходят хребты высочайших гор, простираются обширные плодородные равнины и тянутся столь же обширные пустыни... – А на луне? – спросил я
|