|
3.2. Наземные нагрузки на ракету
Наземные нагрузки в положении на старте и при транспортировке зависят от назначения ракеты и условий, в которых производится ее эксплуатация и подготовка к пуску.
Следует отметить, что в случае транспортировки ракеты на очень большие расстояния может возникнуть потребность дополнительной проверки ее элементов на прочность и вибрацию.
* * *
1. Старт
В положении на старте элементы конструкции ракеты нагружаются собственным весом и весом топливных компонентов.
При определении нагрузок для этого случая следует учесть и возможные ветровые нагрузки, стремящиеся опрокинуть ракету или сдвинуть ее. Критическое значение сдвигающей нагрузки определяется из соотношения
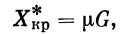 |
(40) |
где μ — коэффициент трения между опорными поверхностями. Наименьшее значение опрокидывающей нагрузки Хкр в зависимости от угла наклона оси ракеты к вертикали ϑ и угла φ (рис. 28, 29) можно найти, составив уравнение моментов всех сил относительно оси опрокидывания (например, ВС), предварительно определив опорные реакции.
Таким образом, следует, что
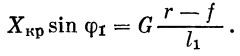
Здесь
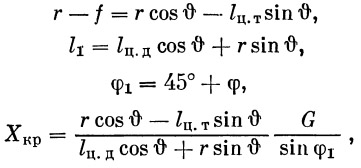 |
(41) |
где lц.т — расстояние от опорной поверхности ракеты до центра тяжести, lц.д — расстояние от опорной поверхности до центра давления, r — расстояние от оси ракеты до оси опрокидывания.
| |
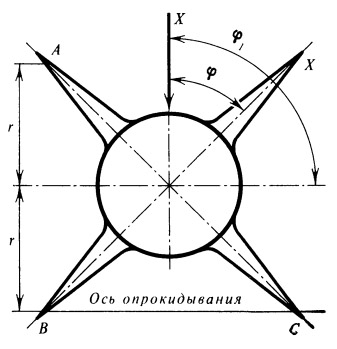
Рис. 28.
К расчету опрокидывающей нагрузки, действующей
на ракету на стартовом столе (вид сверху) |
|
| |
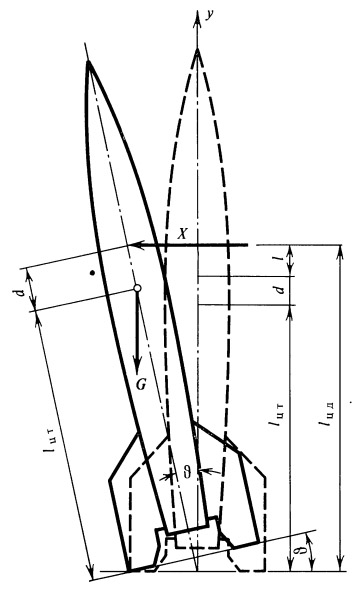
Рис. 29.
К расчету опрокидывающей нагрузки, действующей
на стартовом столе (вид сбоку) |
|
В этом случае опорные реакции равны
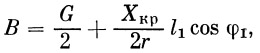 |
(42) |
Кроме того, наличие составляющей Хкр cos φ1 приводит к перераспределению реакций между опорами В к С.
Все вышеприведенное имеет в основном значение для незаполненной ракеты.
* * *
2. Транспортировка
При транспортировке ракеты по железной дороге имеют место как осевые, так и поперечные перегрузки статического и динамического характера. Осевая перегрузка возникает от изменения скорости движения поезда. Наибольшее значение ее будет в случае экстренного торможения:
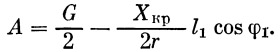 |
(43) |
Длина пути торможения находится по Короткевичу («Расчет и конструкция вагонов»):
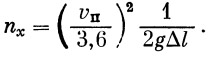
где
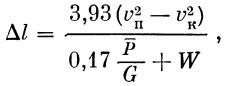
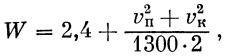 — при однорежимном торможении, — при однорежимном торможении, 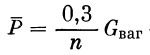 — при двухрежимном, n — число тормозных колодок, vn — скорость поезда в км/сек, Δl — путь торможения в м, vк — конечная скорость торможения. — при двухрежимном, n — число тормозных колодок, vn — скорость поезда в км/сек, Δl — путь торможения в м, vк — конечная скорость торможения.
Статическая поперечная перегрузка возникает при движении поезда по кривой с радиусом R:
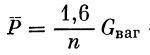 |
(44) |
Вследствие ударов колес вагона о рельсы в местах их стыков и погрешностей в изготовлении колес возникает вертикальная инерционная динамическая нагрузка, величина которой может быть определена лишь опытным путем и составляет примерно, по опытам НИИЖТ, 50-60%) G:
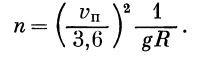 |
(45) |
Указанные мгновенные силы инерции при наличии рессор превращаются в более или менее длительную нагрузку, т. е. ударная нагрузка превращается в вибрацию с частотой, пропорциональной числу осей вагона, в котором транспортируется ракета, и скорости движения:
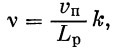 |
(46) |
где k — число осей в вагоне, Lp=12,5 м — длина рельса (например, при vп=80 км/час и k=4 v=7,1 гц).
При перевозке на значительные расстояния (L0) эксплуатационное число циклов колебаний будет равно
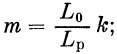 |
(47) |
так, при длине пути L0=10000 км получаем
m=3,2 • 106 циклов.
Коэффициенты перегрузок для случаев транспортировки по шоссейным и грунтовым дорогам можно определить лишь опытным путем. Величины их в большинстве случаев зависят от случайных факторов, влияние которых можно уменьшить при правильной эксплуатации.
* * *
3. Подъем ракеты
При подъеме ракеты краном возможны динамические нагрузки в поперечном направлении при пуске и остановке. Величина этих нагрузок зависит как от конструкции тормозных устройств крана, так и от выполнения правил эксплуатации его. По «Нормам прочности для самолетов» этот коэффициент принимается равным ny=2.
* * *
3.3. Нагрузки на основные узлы конструкции ракеты
1. Силовая схема ракеты
Движущая сила Р приложена к корпусу ракеты, в котором помещается полезный груз Gп, приборы Gпр и топливные баки (В) и (А). В общем случае линия действия ее не совпадает с осью ракеты вследствие наличия газодинамического и геометрического эксцентриситетов. Поверхностная аэродинамическая нагрузка, возникающая при движении ракеты в атмосфере и создающая лобовое сопротивление Q, характеризуется величиной давления pп, нормального к поверхности, и напряжением трения рt касательным к поверхности корпуса. Массовые силы от агрегатов, находящихся внутри корпуса, обусловленные наличием ускорения, приложены к нему в местах их крепления в виде сосредоточенных или как-то распределенных нагрузок (в зависимости от конструкции крепления).
Инерционная нагрузка от массы самого корпуса распределяется пропорционально площади его сечения и плотности материала. Для выполнения полета по заданной программе в хвостовой части корпуса ракеты имеется система газовых и воздушных рулей и стабилизирующие поверхности, создающие необходимые поперечные нагрузки и моменты. Стабилизатор нагружается поверхностной аэродинамической нагрузкой, значительно превышающей нагрузку от собственной массы. Эта нагрузка передается на корпус в местах крепления к нему стабилизирующих поверхностей. Все нагрузки на отдельные узлы конструкции ракеты определяются в связанной системе координат (х, у, z).
* * *
2. Нагрузки на корпус ракеты
Осевая нагрузка
Осевая нагрузка на корпус равна сумме всех осевых массовых и поверхностных сил. При малых углах атаки можно пренебречь осевой составляющей подъемной силы Y корпуса, т. е. считать, что
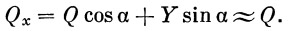
Тогда осевая нагрузка на любое поперечное сечение корпуса ракеты Т в общем виде может быть записана так:
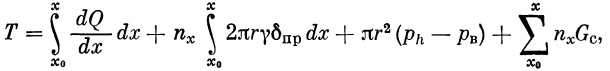 |
(48) |
где x0 — координата носка ракеты, dQ/dx — погонное лобовое сопротивление, r — радиус сечения корпуса, γ — удельный вес материала корпуса ракеты, δпр=Fсеч/2πr — приведенная толщина корпуса ракеты, Fсеч — площадь сечения корпуса ракеты, pв — давление внутри корпуса ракеты, nxGc — сосредоточенная массовая нагрузка на корпус от агрегатов, находящихся внутри его.
Поперечная нагрузка
Равнодействующая всех поверхностных поперечных сил всегда направлена противоположно равнодействующей поперечных массовых сил, т. е. в любом сечении ракеты погонная поперечная нагрузка будет равна
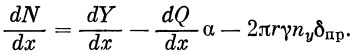 |
(49) |
Сосредоточенные силы будут: Ncny, qynydx, Np, где Nc — сосредоточенная поперечная нагрузка от веса агрегатов, находящихся внутри корпуса ракеты, qy — погонная распределенная поперечная нагрузка от веса агрегатов, находящихся внутри корпуса, dY/dx — погонная подъемная сила, Nр — сосредоточенная поверхностная поперечная нагрузка от рулей.
Интегрируя выражение (dN/dx)ст от x0 до x1 можем определить перерезывающую силу N в любом сечении x1
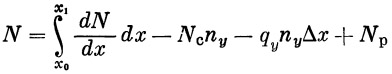 |
(50) |
и изгибающий момент
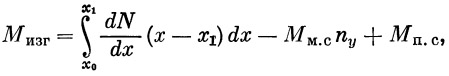 |
(51) |
где Mм.c — сосредоточенный момент в сечении x1 корпуса от веса агрегатов, находящихся в нем; Мп.с — сосредоточенный момент от поверхностных сил.
На конструкцию и узлы крепления агрегатов, находящихся внутри корпуса ракеты, действуют лишь массовые силы, определяемые коэффициентами nх и nу.
Для отдельных элементов конструкции корпуса расчетными могут быть местные нагрузки от действия сосредоточенных сил и местной разности температур, а также нагрузки, зависящие от величины и характера распределения местной поверхностной силы.
| |

Рис. 30.
К расчету нагрузки на топливный бак |
|
Нагрузки на топливные баки
В общем случае, когда в баке имеется жидкость с удельным весом γв и избыточное газовое давление pизб, стенки его нагружаются переменным по длине бака давлением (рис. 30)
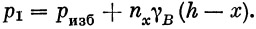 |
(52) |
Наличие поперечной перегрузки пу приводит к несимметричному нагружению стенок бака и по поперечному сечению. Дополнительное давление Δp1 от ny1 будет на одной стороне суммироваться с основным давлением, а на противоположной вычитаться (см. рис. 30):
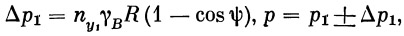 |
(53) |
где R — внутренний диаметр бака.
По оси бака в каждом поперечном сечении его х, лежащем ниже мест крепления бака в осевом направлении х1 действует сила, равная
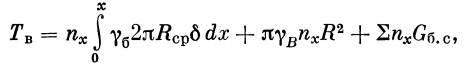 |
(54) |
где
x < x1 < l
Rср — радиус средней поверхности корпуса бака в данном сечении, Gб.c — вес деталей, присоединенных к корпусу бака. Выше мест крепления
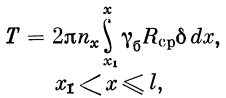 |
(55) |
где l — длина бака.
Дополнительная нагрузка на стенки бака, зависящая от скорости изменения уровня жидкости в баке,
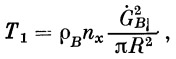 |
(56) |
где ρв— плотность жидкости (В), G — секундный расход жидкости (B)). Нагрузка, зависящая от скорости вытекания из бака жидкости, мала и ею можно пренебречь.
| |
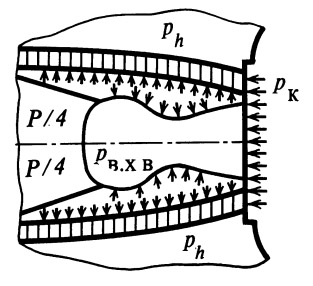
Рис. 31.
К расчету нагрузки на раму двигательной установки |
|
Нагрузки на раму двигательной установки
Рама двигательной установки в осевом направлении нагружается силой (рис. 31)
 |
(57) |
| |
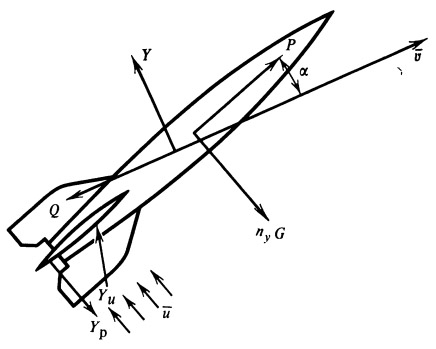
Рис. 32.
К расчету нагрузки на оперение |
|
где Gк.сг — вес камеры сгорания с охлаждающей жидкостью, находящейся в ней, pв.хв — давление внутри хвостового отсека.
В данном случае тягу следует брать с учетом величины Fа (pа—pк) без учета потери ее на газовые рули.
Поперечная нагрузка на раму зависит не только от коэффициента перегрузки ny1 но и от эксцентриситета d тяги Р и углового эксцентриситета тяги Δγ1
Линейный эксцентриситет тяги d приводит к неравномерному загружению стержней рамы.
Нагрузки на оперение
Так как в полете в основном имеет место несимметричное нагружение перьев стабилизатора, то рассматриваем случай наиболее неблагоприятной комбинации на одном из перьев нагрузок: уравновешивающей, маневренной и от неспокойного воздуха (рис.32). Под уравновешивающей нагрузкой мы будем понимать поперечную аэродинамическую силу, пропорциональную углу атаки (или углу рыскания):
| αу = αпр + Δαβр + Δαк + α0 . |
(58) |
Если изменение Δαк носит динамический характер, то αу следует брать равным
αу = αпр + Δαβр + 2Δαк + α0,
где α0 — угол перекоса пера стабилизатора, ΔαРр — дополнительный угол атаки для стреловидного оперения за счет угла рыскания, Δαк — дополнительный угол атаки за счет отклонения оси ракеты от программного положения.
Под маневренной нагрузкой понимают нагрузку, пропорциональную угловой скорости вращения ракеты. Маневренная нагрузка может быть выражена через средний угол атаки:
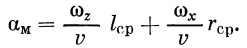 |
(59) |
Следовательно, суммарная нагрузка на перо будет равна
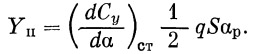 |
(60) |
Здесь
αр = αu + αу + αм,
где αu — угол атаки при воздействии ветра.
При определении сил, действующих на корпус хвостового отсека, необходимо рассмотреть случай совместного нагружения всех перьев стабилизатора.
1. Случай несимметричного нагружения перьев горизонтального оперения. В этом случае берут нагрузку на одно перо, равную
Y1 = Y + ΔY1 ± Yв.р
а на другое
Y2 = Y + ΔY2 ± Yв.р |
(61) |
где Y — средняя нагрузка на перо, определяемая углом атаки
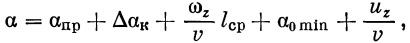 |
(62) |
ΔY — дополнительная нагрузка, равная
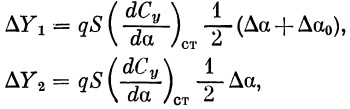 |
(63) |
где
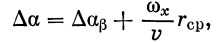
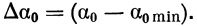
Степень несимметричности нагрузки на оперение определяем как отношение
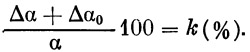
2. Случай совместного нагружения горизонтального и вертикального оперения предусматривает, помимо нагружения горизонтального оперения нагрузкой Y1=Y2, несимметричную нагрузку вертикального оперения при углах рыскания
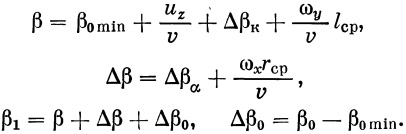 |
(64) |
3. Коэффициент безопасности
При расчете конструкции на наиболее возможные при эксплуатации нагрузки необходимо, чтобы напряжения в ответственных узлах, деформации которых могут повлиять на управляемость или на аэродинамические характеристики ракеты, не превосходили значительно предела пропорциональности σпр, а в узлах малоответственных — предела текучести σs.
При расчете на разрушающие нагрузки это достигается введением коэффициента запаса прочности
где σв — временное сопротивление материала, σр — расчетное напряжение.
Примечание. Механические свойства материалов необходимо брать при эксплуатационном температурном режиме.
Возможное отклонение расчетных нагрузок от действительных из-за неточности исходных баллистических и аэродинамических данных и из-за приближенности самой методики определения нагрузок следует учесть некоторым коэффициентом «незнания» (fn1), определяемым в каждом конкретном случае. Отклонение расчетной схемы от действительной картины загружения, а также различного рода производственные недостатки конструкции должны быть учтены «технологическим» коэффициентом безопасности fт, тогда коэффициент безопасности будет равен
Следовательно, расчетная разрушающая нагрузка будет равна произведению расчетной эксплуатационной нагрузки на коэффициент безопасности
|