|
ЛЕКЦИЯ ВТОРАЯ

Для получения приближенной зависимости* L=f(v) или v=f(L) воспользуемся выражением, дающим дальность эллиптического участка Lэл (или соответствующий ей центральный угол 2β) в функции параметра v и угла θ:
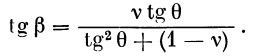 |
(1) |
Здесь
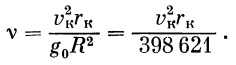 |
(2) |
Определим оптимальное значение угла θ. Для этого возьмем производную от tg β по переменной tg θ и приравняем нулю:
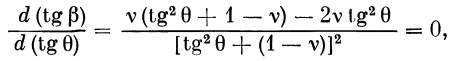
откуда следует, что
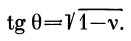 |
(3) |
Подставляем значение tg θ в (1):
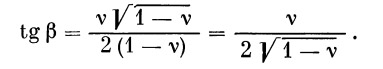
Отсюда легко получить эллиптическую дальность
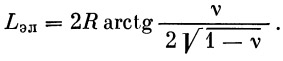 |
(4) |
Так как высота конца активного участка по сравнению с радиусом Земли мала, то колебание rк влияет на v несильно, поэтому для приближенных расчетов мы принимаем rк=R, a
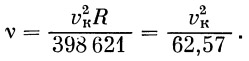 |
(5) |
Подстановка полученного значения v в (4) дает
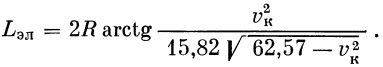 |
(6) |
_____________________
* Здесь вместо lполн, lэл, θ0, v0, r0, β0 введены обозначения соответственно L, Lэл, θ, vк, rк, β
Если дугу 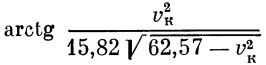 брать в градусах, то брать в градусах, то
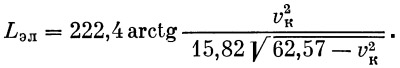 |
(7) |
Значение vк можно получить, имея заданную дальность, из формулы (7), но можно значение vк получить следующим образом. Из (3) имеем
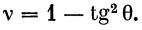
Подставляя это значение в (1), получим
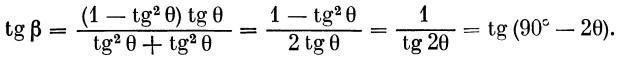
Вспомогательные формулы:
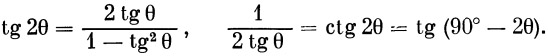
Отсюда
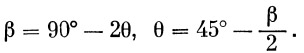 |
(8) |
Далее, из (1) и (3) имеем
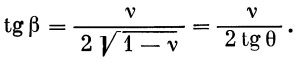
Отсюда v=2tg β tg θ.
Подставляя θ из (8), a v из (5), получим
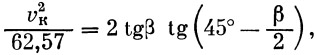
но β=Lэл/2R, поэтому 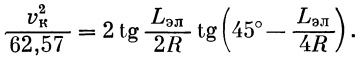 . .
Если подставить сюда R=6371 км и углы выразить в градусах, то окончательно получим
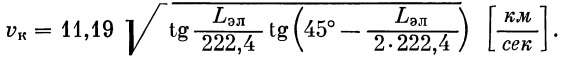 |
(9) |
Зависимости (7) и (9) связывают конечную скорость с эллиптической дальностью. Для определения полной дальности введем коэффициент k таким образом, чтобы L=kLэл.
Зависимость k = f (L) получена на основании обработки целого ряда расчетов и приводится на рис. 6. Зависимость L = f (vк) приводится на рис. 7.
Задачей метода приближенного расчета является получение зависимости скорости на активном участке и полной дальности ракеты от ее основных параметров.
В качестве таких параметров мы выбираем:
1) μ — отношение текущего веса к начальному весу,
2) Pуд п — удельная тяга в пустоте,
3) v0 — отношение начального веса к начальной тяге,
4) Рм — нагрузка на мидель,
5) ΔPуд — разница между удельными тягами в пустоте и на уровне моря,
6) θ — угол наклона касательной к траектории относительно начального горизонта.
| |

Рис.6.
Зависимость коэффициента полной дальности от дальности
1 — T=210 сек; 2 — 180; 3 — 150; 4 — 120 сек |
|
Для получения метода приближенного расчета воспользуемся уравнениями движения ракеты, учитывающими лишь основные силы, действующие в полете (углами атаки пренебрегаем):
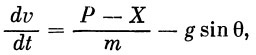 |
(10) |
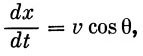 |
(11) |
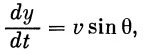 |
(12) |
где m — масса ракеты, P — тяга, g — ускорение силы тяжести, X — сила лобового сопротивления.
Для тяги принимается следующий закон изменения с высотой:
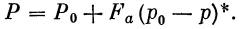 |
(13) |
Заметим, что P достигает максимального значения при p=0, т.е. в пустоте:
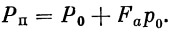 |
(14) |
Сила сопротивления воздуха определяется как
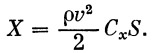 |
(15) |
Запишем уравнение (10) в несколько ином виде:
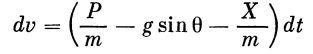 |
(16) |
__________________
* Здесь вместо Sa принято обозначение Fa.
| |
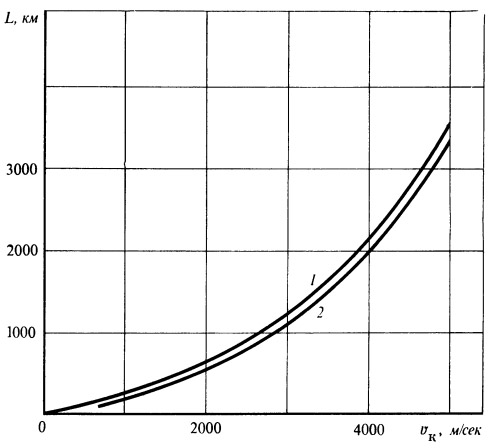
Рис. 7.
Зависимость полной дальности от конечной скорости
1 — T=210 сек; 2 — 120 сек |
|
и введем следующие обозначения:
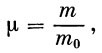 |
(17) |
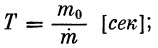 |
(18) |
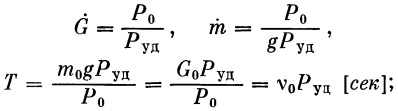
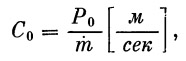 |
(19) |
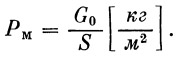 |
(20) |
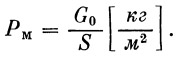 |
(21) |
Здесь μ — безразмерный коэффициент, характеризующий относительный вес ракеты, т. е. показывающий, какую долю от первоначального веса сохраняет ракета в рассматриваемый момент. Коэффициент μ теоретически может изменяться в пределах от 1 до 0. В момент старта μ=1, в момент выключения двигателя μ принимает минимальное для данной траектории значение; μ в известной степени характеризует совершенство конструкции с точки зрения максимального облегчения несущих и силовых элементов и наиболее рационального использования «мертвого веса» конструкции. Величина 1—μ показывает, какая доля от первоначального веса израсходована к рассматриваемому моменту.
T — идеальное время, т.е. время работы двигателя такой «идеальной» ракеты, у которой конечное значение μк=0. Другими словами, Т — время, в течение которого при данном постоянном секундном расходе сгорало бы количество топлива, равное по весу стартовому весу ракеты.
μ, Т и t связаны между собой определенными зависимостями. Из (17) и (18) имеем
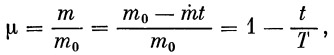 |
(22) |
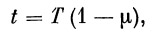 |
(23) |
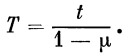 |
(24) |
C0 — эффективная скорость истечения продуктов сгорания у Земли; вычисляется как отношение абсолютной тяги у Земли (за вычетом потерь на управление) к секундному расходу массы.
Cп — эффективная скорость истечения продуктов сгорания в безвоздушном пространстве; вычисляется как отношение абсолютной тяги в пустоте (за вычетом потерь на управление) к секундному расходу массы.
С0 и Сп не являются истинными скоростями истечения газов из сопла, как это видно из следующих рассуждений.
Полная тяга может быть записана в виде
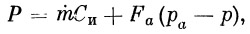
где Cи — истинная скорость истечения, Fa — площадь выходного сечения сопла, pа — давление газа на срезе сопла, p — наружное давление.
Из последнего выражения следует
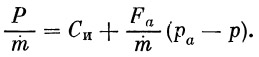
Если обозначить 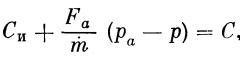 то то 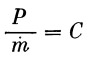 и будет эффективной скоростью истечения. и будет эффективной скоростью истечения.
Следует заметить, что эффективная скорость истечения совпадает с истинной только при расчетном режиме работы двигателя, т. е. на расчетной высоте, которая определяется равенством pа=p.
Под секундным расходом массы понимается суммарный расход всех компонентов, участвующих в уменьшении массы ракеты. Эффективные скорости истечения С0 и Сп физически означают величину абсолютной тяги в кг, приходящейся на каждую единицу секундного расхода массы.
Если соответствующие значения абсолютных тяг относить не к секундному расходу массы, а к секундному расходу веса, то получим удельные тяги
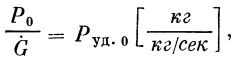 |
(25) |
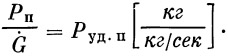 |
(26) |
Из (19) и (25) можно получить, что
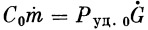
или
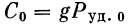 |
(27) |
и аналогично
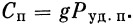 |
(28) |
Рм — нагрузка на мидель, или поперечная нагрузка, т. е. стартовый вес в кг, приходящийся на площадь наибольшего поперечного сечения ракеты. Как будет показано ниже, потеря скорости на преодоление сопротивления воздуха зависит от поперечной нагрузки. Чем больше поперечная нагрузка, тем меньше потери скорости при прохождении ракетой атмосферы. Поэтому Рм желательно иметь по возможности большим, не причиняя ущерба, однако, другим характеристикам ракеты.
Рассмотрим каждый член выражения (16) в отдельности. Первый член Р/m. Учитывая (13), (14) и (17), имеем
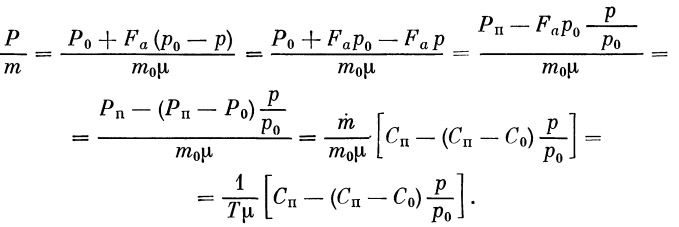
Второй член оставляем в том же виде. Третий член Х / m:
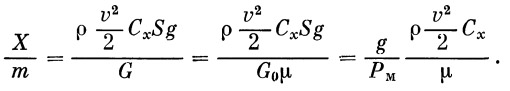
Подставляя эти значения в уравнение (16), получим
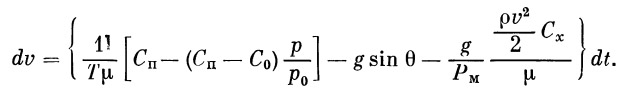 |
(28a) |
Из (23) имеем
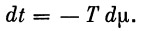 |
(29) |
Поэтому окончательно
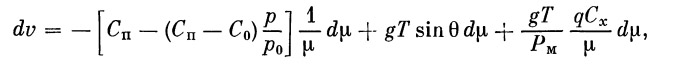
где скоростной напор ρv2/2 обозначен через q.
Проинтегрируем полученное уравнение в пределах от v0 до v и от μ0 до μ:
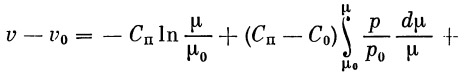
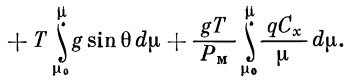
В качестве нижнего предела интегрирования примем параметры движения в момент старта, т. е.
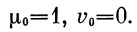
Получим
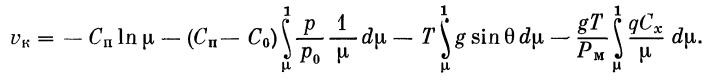 |
(30) |
Обозначаем в уравнении (30)
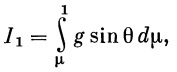 |
(31) |
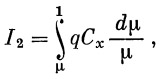 |
(32) |
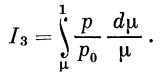 |
(33) |
Таким образом, для вычисления скорости получим следующее основное выражение:
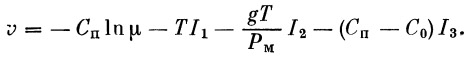 |
(34) |
Член — Cп ln μ определяет скорость ракеты, движущейся при условии отсутствия притяжения Земли и атмосферы. Скорость истечения газов в этом случае (а следовательно, и тяга) будет постоянной и максимальной.
Членом TI1 определяется потеря скорости, вызванная действием силы тяжести. Эта потеря является наиболее существенной среди всех других и должна быть учтена в первую очередь.
Член 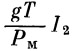 составляет потерю скорости на преодоление сопротивления воздуха. Относительная величина потери скорости на преодоление сопротивления воздуха составляет потерю скорости на преодоление сопротивления воздуха. Относительная величина потери скорости на преодоление сопротивления воздуха 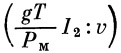 тем меньше, чем мощнее ракета. тем меньше, чем мощнее ракета.
Являясь важным фактором при определении скорости небольших ракет (например, 2ПБ), эта потеря постепенно уменьшается, составляя для сверхдальних ракет до 2—3% и меньше, как это показано на рис. 11.
Так как ракета движется в атмосфере, причем давление атмосферы с высотой переменно, то и тяга, согласно (13), будет переменной, увеличиваясь от минимального наземного значения до максимального в пустоте.
Поэтому член Сп ln μ дает преувеличенное значение скорости.
Член (Cп—C0)I3 дает соответствующую поправку, учитывающую это обстоятельство.
Если заданы все характеристики ракеты, то вычисление первого члена уравнения (34) никаких затруднений не вызывает.
Вычисление второго члена уравнения (34) связано с определением численного значения h. Для этого нам необходимо знать g и sinθ в функции μ или t.
В первом приближении и с достаточным основанием (высоты на активном участке по сравнению с радиусом Земли малы) можно считать g=const, чего нельзя допустить относительно θ. Недопустимо также оценивать его каким-либо средним значением, не рискуя сделать грубую ошибку. В то же время известно, что характер зависимости θ=θ(μх) для всех дальних ракет имеет примерно одинаковый вид. Известно также, что небольшие изменения зависимости θ=θ(μ) на конечную скорость влияют незначительно.
Опыт работы показывает, что все зависимости θ=θ(μ), выбираемые из условий, о которых речь будет далее, имеют форму, приближающуюся к квадратной параболе.
Поэтому, желая избавиться от большого числа вариаций зависимости θ=θ(μ) и тем самым облегчить вычисления и сделать применимыми их для более общего случая, целесообразно принять для всех траекторий единую зависимость.
Если принятая зависимость после соответствующих расчетов и сравнений с более точными методами покажет удовлетворительную точность, то ее можно будет использовать во всех дальнейших расчетах без изменений. Такая зависимость, как уже отмечалось, может быть принята в виде квадратной параболы, на которую наложены следующие условия.
1. В момент времени t1 (μ=μ1), соответствующий началу криволинейного полета (начало «программы»), угол θ=90°.
2. Необходимый конечный угол наклона касательной к траектории достигается в момент t2, соответствующий μ=μ2.
3. В этой точке производная угла θ по времени (и по μ) равна нулю.
В промежутке между μ=μ1 и μ=μ2 угол θ изменяется по квадратной параболе. После μ2 угол наклона касательной к траектории остается неизменным до момента выключения двигателя.
При этих условиях уравнение параболы удобно записать в виде:
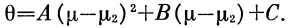 |
(35) |
Коэффициенты А; В и С легко определить из указанных трех условий.
Для того чтобы задача была более конкретной, необходимо задаться определенными значениями μ и μ2, постоянными для всех возможных случаев расчета. Можно считать установленным, что вертикальный участок продолжается до значений μ1, близких к 0,95. Поэтому вполне естественно принять μ1=0,95.
Далее, активные участки почти всех ракет дальнего действия обладают тем свойством, что после μ=0,4÷0,5 траектория либо прямолинейна, либо очень близко подходит к прямой. В то же время μк больше, чем 0,3—0,4, как правило, не встречается.
Исходя из этого, можно участки траектории после μ=0,45 считать для всех ракет прямолинейными и отличающимися друг от друга только величиной угла наклона. Поскольку мы заинтересованы стрельбу вести всегда при оптимальных углах, то θк для разных траекторий будут разные.
Таким образом, потери скорости от силы тяжести будут функцией конечного угла θк и μ.
Подставим в уравнение (3)5) μ2=0,45 и найдем производную угла θ по переменной μ:
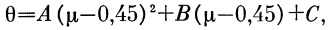 |
(36) |
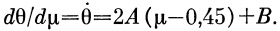 |
(37) |
Для определения коэффициентов А, В и С имеем следующие три условия:
1) μ=0,95, θ=π/2;
2) μ=0,45, θ=θк;
3) μ=0,45, θ=0.
Используя третье условие, получим
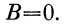
Тогда уравнение (36) примет вид
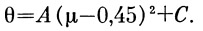
Используя второе условие, найдем, что
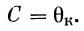
И, наконец, первое условие позволяет определить коэффициент А:
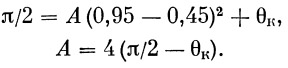
Подставляя все найденные коэффициенты в уравнение (36), получим зависимость
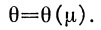
В окончательном виде
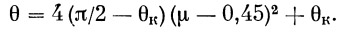 |
(38) |
Теперь нетрудно вычислить I1 в зависимости от μ для различных значений θк.
Значения интеграла
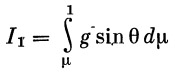
приведены в табл. 1 и на рис. 8, которыми и будем в дальнейшем пользоваться.
Займемся теперь интегралом I2, выражающим влияние сопротивления воздуха:
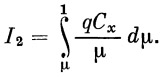
Для того чтобы вычислить этот интеграл, необходимо заранее знать q=ρv2/2 и Cx(М, h) в функции μ. Для получения этих зависимостей мы воспользуемся первыми двумя членами уравнения (34), дающими скорость в функции μ при условии отсутствия атмосферы.
Таблица 1
Обозначим
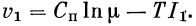 |
(39) |
Тогда высоты, соответствующие этим скоростям, будут
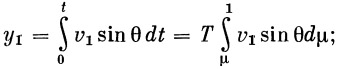 |
(40) |
v1 и y1 назовем скоростью и высотой первого приближения. Зная v1 и y1 легко вычислить
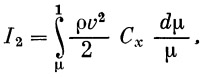
При вычислении I2 вместо v будем подставлять v1; ρ1 будем брать не по истинным значениям y, а по y1; Cx будет соответственно определяться по v1 и y1.
Большое количество расчетов, проведенных с целью определения I2, позволило установить следующую эмпирическую зависимость: значения интеграла, соответствующие одному и тому же значению скорости, нанесенные на график в зависимости от величины
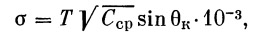 |
(41) |
имеют вокруг некоторой средней кривой незначительный разброс. Здесь
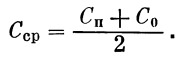
| |
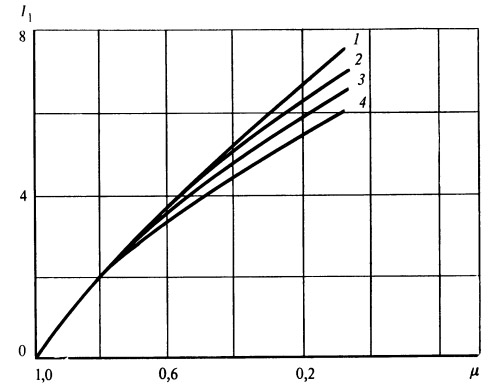
Рис. 8.
Зависимость интеграла гравитационных потерь
от относительного конечного веса
1 — θ=45°; 2 — 40°; 3 — 35°; 4 — 30° |
|
Поэтому оказалось возможным построить зависимости
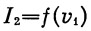
при параметре σ (рис. 9).
Значения I2 получаются достаточно близкими к действительным, так как при вычислении скорости берутся завышенные (из первого приближения), а плотности — заниженные (ввиду завышенных высот первого приближения).
Таким образом, для определения потери скорости от сопротивления воздуха достаточно вычислить
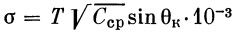
и, взяв его в качестве параметра, найти I2 в зависимости от заранее известной из первого приближения скорости v1. Полученное I2 умножить затем на величину gT/Pм, которой характеризуется каждая отдельно взятая ракета. Нужно заметить, что при вычислении I2 для всех ракет были приняты одинаковые коэффициенты Сх. Это обстоятельство, однако, не приводит к значительным ошибкам по следующим соображениям.
1. Для всех ракет нормальной баллистической схемы коэффициенты Сx примерно одинаковы.
2. Зависимости Cx(M, h), по которым ведутся точные расчеты для конкретных ракет, сами по себе обладают значительными ошибками.
| |

Рис. 9.
Зависимость интеграла аэродинамических потерь
от конечной скорости |
|
3. Влияние сопротивления воздуха для ракет, вообще говоря, невелико. Это в особенности относится к мощным ракетам, предназначенным для больших дальностей. Эти потери для современных ракет выражаются в потере скорости 4—5%. Поэтому ошибки за счет Сх оказывают незначительное влияние [на vк]. Остается еще одна поправка, которая учитывает изменение тяги с высотой и выражается в виде
(Cп—C0)Iз .
Для вычисления I3 необходимо знать [зависимость]
p(p0=f(μ) ,
которая будет известна, если известна высота y в функции μ. Было проведено большое количество расчетов с целью определения I3, причем высоты y брались из второго приближения. Высотой второго приближения мы называем высоту, полученную при интегрировании уравнения (34) с учетом первых трех членов, т. е.
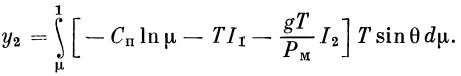 |
(41a) |
В результате обработки этих расчетов удалось для величины η,
равной
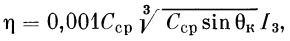
установить эмпирическую зависимость.
| |
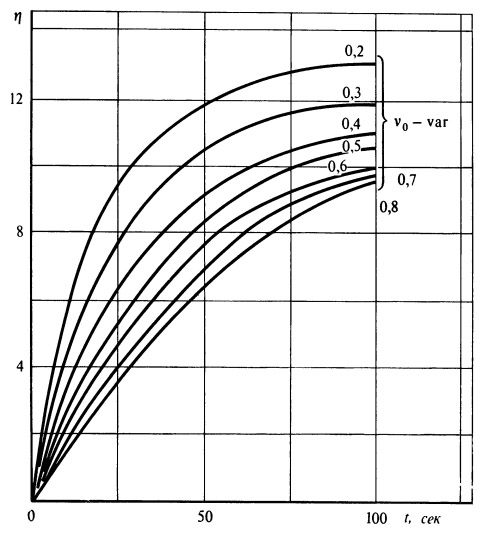
Рис. 10.
Зависимость параметра, пропорционального
интегралу потерь на преодоление противодавления,
от времени |
|
Для определения параметра η необходимо воспользоваться рис. 10,
где η дается в зависимости от времени полета t и v0:
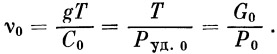
Таким образом, имея конкретную ракету, вычисляем для нее v0 и находим для интересующего нас момента времени параметр η. Деля η на
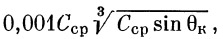
получаем I3:
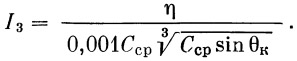 |
(42) |
| |

Рис. 11.
Зависимость скорости и ее абсолютных и относительных потерь от относительного конечного веса 1, 2 — Δv1; 3 — Δv2; 4 — Δv3; 5 — (Δv2)/v; 6 — (Δv3)/v; 7 — (Δv1)/v |
|
| |
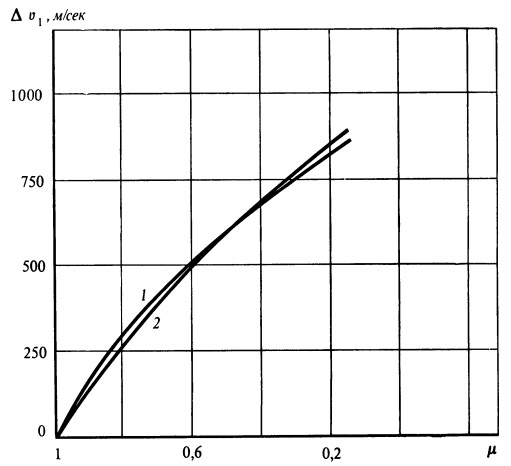
Рис. 12.
Зависимость гравитационных потерь скорости, вычисленных
разными методами, от относительного конечного веса
1 — численное интегрирование; 2 — приближенная методика
|
|
| |

Рис. 13.
Зависимость аэродинамических потерь скорости,
вычисленных разными методами, от относительного
конечного веса
1 — приближенная методика; 2 — численное
интегрирование |
|
| |

Рис. 14.
Зависимость потерь скорости на преодоление
противодавления атмосферы, вычисленных
разными
методами, от относительного конечного веса
1 — численное интегрирование; 2 — приближенная
методика |
|
Произведение I3(Cп—C0) дает нам искомую потерю скорости на преодоление противодавления воздуха.
После определения всех потерь по формуле (34) вычисляем конечную скорость.
На рис. 11 приводятся кривые, позволяющие на частном примере проследить за изменением скорости в зависимости от μ и соотношением между отдельными членами формулы (34)*.
______________________
* Результаты получены при следующих начальных условиях:
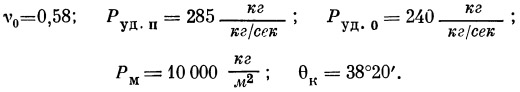
На графике вниз отложены потери скорости Δv1, Δv2 и Δv3, отнесенные к истинной скорости v.
Здесь обозначено:
Δv1=TI1 — потеря скорости на преодоление силы тяжести, Δv2 = ((gT) / Pм) I2 — потеря скорости на преодоление силы сопротивления воздуха, Δv3= (Сп—С0)I3 — потеря скорости на преодоление противодавления атмосферы.
На рис. 12—14 дается сравнение отдельных потерь Δv1=f(μ), Δv2=f(μ), Δv3=f(μ), вычисленных для частного примера двумя методами, а именно численным интегрированием и только что изложенным методом.
На рис. 15 приводится сравнение конечных скоростей, вычисленных этими же двумя методами.
По уравнению (34) может быть построена зависимость
vк = f (μк)
По уравнениям (7) и (9) из зависимости
vк = f (μк)
может быть построена зависимость
Lэл = f (μк)
Вводя коэффициент k, изменение которого представлено на рис. 6, можно получить зависимость полной дальности полета от величины μк.
Получение по заданной величине дальности значения μк позволяет перейти в дальнейшем к первому определению стартового веса.
|