|
f) Проект Гоманна полета в мировом пространстве.
Немецкий инженер Вальтер Гоманн, в своей книге «Досягаемость небесных тел» (Мюнхен 1925 г.), исследует вопрос о возможности полета ракетного снаряда в межпланетное пространство и, в частности, на Луну, Венеру и Марс, а также исследует условия спуска снаряда обратно на Землю.
Ниже приводятся главнейшие результаты его исследования. Полный-же перевод его работы приводится отдельно в специальной книге.
Сочинение заключает в себе пять глав:
1-я глава. – Подъем с земли.
2-я " Спуск на землю.
3-я " Свободный полет в пространстве.
4-я " Облет других небесных тел.
5-я " Спуск на другие небесные тела.
Подъем с земли: Автор исследует влияние разных собственных ускорений ракеты при взлете и учитывает влияние земного притяжения при разных скоростях извержения газов из ракеты. В нижеследующей таблице даны результаты его подсчетов, при чем сопротивление воздуха пока – в расчет не принимается.
ТАБЛИЦА
Полет с земли без учета сопротивления воздуха,
Собственное ускорение
снаряда m/sec2 |
15 |
20 |
25 |
30 |
40 |
50 |
100 |
200 |
Подъем над центром
земли в km r 1
|
10600 |
9510 |
8860 |
8490 |
7950 |
7640 |
7000 |
6680 |
Скорость полета в конце
извержения газов v1 m/sec. |
8660 |
9150 |
9470 |
9680 |
10000 |
10200 |
10650 |
10890 |
| Продолжительность полета, до окончания иавержения газов t1sec |
1192 |
762 |
565 |
448 |
319 |
248 |
117 |
57 |
Отношение
начальной
массы сна-
ряда к
конечной
(при окончании
взрывов) – при
скорости
извер-
жения газов C |
C = 1000 m/sec | 58700000 | 4160000 | 1545000 | 675000 | 346000 | 240000 | 120300 | 89130 |
| C = 1500 " | 149000 | 25000 | 12000 | 7750 | 4950 | 3840 | 2400 | 2000 |
| C = 2000 " | 7570 | 2010 | 1160 | 825 | 587 | 495 | 347 | 299 |
| C = 2500 " | 1270 | 438 | 282 | 2l6 | 164 | 143 | 108 | 95,5 |
| C = 3000 " | 388 | 159 | 110 | 88 | 70 | 62 | 49 | 44,7 |
| C = 4000 " | 87,3 | 44,8 | 34,1 | 28,7 | 24,2 | 22, | 18,7 | 17.2 |
| C = 5000 " | 35,7 | 20,9 | 16.7 | 14,6 | 12,8 | 11,9 | 10,4 | 9.8 |
| С =10000 " | 6,0 | 4.6 | 4,1 | 3,8 | 3,6 | 3.5 | 3,2 | 3,1 |
При вычислении этой таблицы Гоманн принимает, что ускорение силы земной тяжести на разных высотах постоянно и равно
gm = (2g0 + g1) / 3,
где g0 – уск. силы тяжести у поверхности земли,
g1 на расстоянии r1 от центра земли.
Кроме того предполагается, что в каждый момент извергаемая масса пропорциональна остающейся массе снаряда и скорость извержения газов постоянна.
Конечная скорость v1 данная в таблице, соответствует случаю, когда, на расстоянии r1 снаряд перестает двигаться ускоренно (теряет собственное ускорение), но в то же время обратно не упадет на землю под влиянием ее притяжения.
Гоманн принимает допустимую для человека величину собственного ускорения снаряда 30 m/sec2, а скорость извержения газов – 2000 m/sec и тогда отношение начальной массы снаряда к конечной (к началу свободного полета и без учета сопротивления воздуха) будет по таблице 825.
Сопротивление воздуха изменяет условия подъема, уменьшая ускорение взлета на величину около 2,4 m/sec2, которое вместо ранее допущенного будет теперь 30 – 2,4 =27,6 m/sec2. Благодаря этому повышается и отношение начальной и конечной масс снар я д а, которое для разных ускорений и скоростей извержения дано в следующей таблице:
ТАБЛИЦА
Полет с земли с учетом сопротивления воздуха.
| Ускорение m/ sec 2. | 30 | 100 | 200
|
| Время подъема t / sec, | 456 вместо 448 | 123 Вместо 117 | 64 вместо 57 |
Скорость
извержения
газов С m/sec. |
С = 2000 | 933 " 825 | 468 " 347 | 602 " 299 |
| С = 2500 | 235 " 216 | 138 " 108 |
166 " 95,5 |
| C = 3000 |
95 " 88 |
60 " 49 | 71 " 44,7 |
| C = 4000 | 30 " 28,7 |
22 " 18,7 |
25 " 7,2 |
| С = 5000 |
15 " 14,6 | 12 " 10,4 |
13 " 9,8 |
В дальнейшем Гоманн принимает для своих подсчетов цифру 933.
Спуск на землю. Для облегчения спуска на землю Гоманн предлагает к летящему со скоростью 11,1 km/sec из мирового пространства снаряду приделать тормозящие поверхности, которые задерживали бы его полет в земной атмосфере, и, кроме того, самый спуск на землю производить не радиально, а по спиралям, описывая вокруг земли все меньшие и меньшие эллипсы, верхушки которых пронизывали бы земную атмосферу на высоте 75 km и постепенно бы тормозили скорость полета, пока она не уменьшится до безопасной для планирующего спуска на землю.
На черт. 185 показаны эти эллипсы; скорости полета снаряда в точке А на высоте 75 km над землей для разных эллипсов будут следующие:
Подход по параболе v '. . . 11,1 km/sec.
1-й эллипс . . . . . . . . . . . . . 10,4 "
2-й " . . . . . . . . . . . . . 9,8 "
3-й " . . . . . . . . . . . . . 9,2 "
4-й " . . . . . . . . . . . . . 8,6 "
5-й " . . . . . . . . . . . . . 8,1 "
Круг . . . . . . . . . . . . . . . . . . 7,85 "
| |
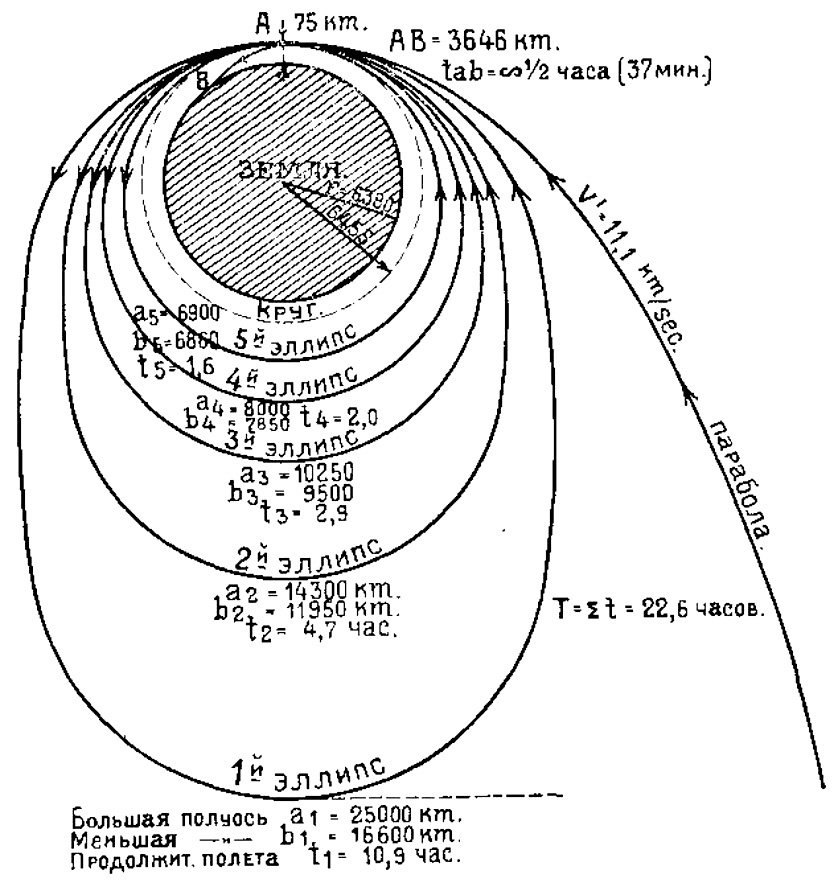
Черт. 185. Спуск космической ракеты на землю по Гоманну. |
|
Последняя скорость соответствовала бы движению снаряда вокруг земли по кругу, если бы не было сопротивления воздуха. Далее полет переходит в планирование АВ длиною 3646 km.
На черт. 185 приведены данные о размерах эллипсов и продолжительности полета по ним. Продолжительность всего спуска занимает 22,6 часа.
Кроме подхода к земле с параболы по эллипсам, Гоманн рассматривает еще прямой переход с параболы на круг, высотою 75 km над землей. Для этого придется перейти с параболы сначала на принудительное движение по кругу (с замедлением движения), описав путь в земной атмосфере длиною 2000 km в 3,63 мин. и затем, достигнув скорости 7,85 km/sec, соответствующей свободному движению по кругу, произвести планирующий спуск, как и раньше. Однако, при этом получатся большие замедления и нагревание снаряда. Для избежания опасности нагревания стенок снаряда при трении о воздух Гоманн предлагает делать их снаружи ребристыми, чтобы увеличить поверхность передачи тепла в воздух и, кроме того, увеличить число облетов по спирали, именно: для скоростей
от 11,1 до 7,85 km/sec . . . . . . . . 6 облетов.
" 7,85 " 4 " . . . . . . . . 3,5 "
" 4 " 0 " . . . . . . . . 0,5 "
_________________
Всего . . 10 облетов.
При этом вся энергия торможения предполагается переходящей в тепло и передающейся снаряду. В действительности число облетов будет где-то посредине между ранее (5) и теперь (10) полученными случаями.
Свободный полет в пространстве. На основании результатов подсчета, произведенного Гоманном в главе 1-й своего труда, он вычисляет скорости v1 полета при прекращении извержения газов, при которых снаряд улетит от земли и более на нее не возвратится. Для обратного же возвращения необходимо во время свободного полета сделать направляющий взрыв, который изменил бы скорость полета. Например, для того, чтобы снаряд, поднявшись на высоту 800000 km над землей, не улетел дальше, а стал бы возвращаться обратно, падая прямо на землю, необходимо уже заранее замедлить скорость, для чего следует потратить взрывчатое вещество, равное 0,11 массы снаряда. Если же мы желаем, чтобы он с этой высоты не падал на землю, а летел бы вокруг нее, описывая эллипс, необходимо на высоте 800000 km произвести еще направляющий взрыв, истратив еще вещество массы, равное 0,09 массы снаряда, который дал бы изменение скорости на 0,09 km/sec.
Таким образом, полет в мировое пространство с обратным движением по элипсу будет происходить следующим образом:
1. Прекращение собственного ускорения снаряда на высоте 8490 km (см. таблицу при ускорении 30 m/sec2),
2. Полет от этого места до начала возвращения с высоты 800000 km. Продолжительность полета 349 часов.
3. Обратный полет по эллипсу с высоты 800000 km до высоты 6455 km (начало торможения). Продолжительность 354 часа.
Итого продолжительность всего полета:
Взлет 8 мин. = ꝏ . . . . . . . . . . . . . 0,2 часа
Свободный полет 349 + 354 = . . 703 "
Спуск . . . . . . . . . . . . . . . . . . . . . . 22,6 "
____________________
Всего около 301/5 дней, т. е. около 1 месяца.
Вес и форма снаряда.
Исходя из расчета 30-дневного полета Гоман определяет вес каюты и припасов для путешествия двух человек следующим образом:
Вес головки снаряда с расчетом на 30 дней полета:
| |
|
|
kg |
| |
а) |
Два человека с одеждой и предметами личного потребления |
200 |
| |
б) |
Пища и вода на 2-х человек, считая по 4 kg в день на человека на 30 дней |
240 |
| |
в) |
Керосин для отопления снаряда на 30 дней и для согревания жидкого кислорода (1,7 + 0,3 = 2 kg) в день |
60 |
| |
г) |
Запас кислорода для дыхания 2-х человек, считая на человека в день 0,6 kg и на горение керосина в день на 1 kg его – 2,7 kg кислорода (2,2,7+2 . 0,6)= 6,6; 6,6 X 30= |
200 |
| |
д) |
Сосуды для хранения жидкого кислорода 0,4 и припасов 0,2
их веса – 200.0,4+(240+60) . 0,2 |
140 |
| |
е) |
Поверхности: тормозящие – 6 m2, несущие – 59 m2, рулевые – 5 /п2, носовая – 10m2, считая по 3 kg/m2= 6 + 59 +5+10=80,803 |
240 |
| |
ж) |
Наружная оболочка снаряда 14,45 m2 по 50 kg/m. |
780 |
| |
з) |
Взрывчатые вещества для направляющих взрывов |
200 |
| |
|
________________________________ |
____ |
| |
|
Итого |
2260 |
Учитывая, что после прекращения собственного ускорения снаряда необходимо будет сделать три направляющих взрыва, расходуя каждый раз 1/10 всего веса, получим вес головки снаряда после прекращения собственного ускорения снаряда – 22601 • 1,13 = 3000 kg.
При начале же планирующего спуска на землю:
3000 – 740 – 240 – 60 – 200 =1760 kg
На черт. 186а изображена вся ракета с головкой (вверху) и запасом взрывчатых веществ (в виде уширяющейся башни).
На черт. 186b – головка с двумя пассажирами изображена отдельно. Она повернута носом вниз, и, наконец, на черт. 186с изображен полет головки при входе из межпланетного полета обратно в земную атмосферу: показан раскрытый парашют (F1), планирующая поверхность (Fo и рули (F). Размеры указаны на чертеже.
При определении размеров ракеты были приняты следующие исходные данные:
Вес головки со снаряжением, как выше указано – 3000 kg = 3f.
Удельный вес взрывчатого вещества 1,5 t/m3.
Ускорение полета при взлете 30 m/sec2.
Скорость извержения газов – с = 2000 m/sec.
Отношение начального веса к конечному (по табл.) 933.
Форма башни рассчитана, исходя из условия равного сопротивления на сжатие в разных ее поперечных сечениях принятого в 1,85 kg/cm2.
Полный вес ракеты при взлете =3 • 933 =2799 t.
Поворот головки снаряда при полете (черт. 186Ь). Для того, чтобы изменить направление полета головки снаряда, необходимо его повернуть так, чтобы взрывная труба расположилась в желаемом направлении. Для этого Гоманн предлагает пассажирам, находящимся внутри снаряда, передвигаться в противоположном направлении,. цепляясь за поручни, прикрепленные внутри стенок. При этом снаряд будет вращаться обратно, пока не расположится в желаемом направлении. Тогда, при помощи взрывной трубы можно произвести взрыв и изменить скорость полета ракеты на желаемую величину.
| |
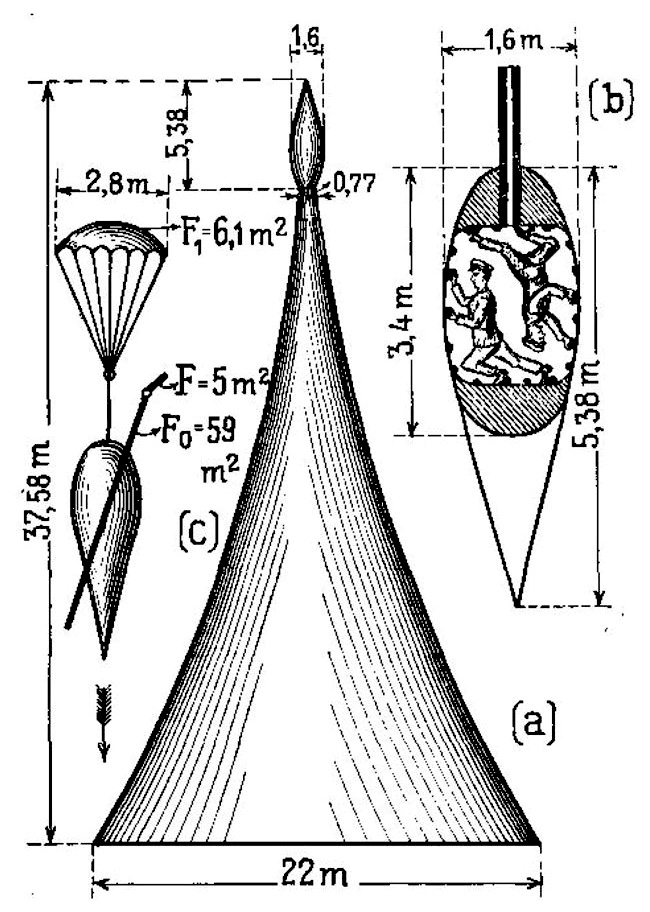
Черт. 186. Ракета Гоманна. |
|
Облет других небесных тел.
а) Облет луны можно осуществить при описанном ранее свободном полете, поднявшись над землею на высоту 800000 km, т. е. почти в два раза дальше, чем от нее отстоит луна и рассчитав время полета так, чтобы при наиболее удаленном положении снаряда от земли луна прошла между ним и солнцем. Направление полета следует принимать к солнцу, чтобы видеть освещенными землю и луну.
б) Облет Венеры. Если снаряд, достигнув высоты 800000 km над землей, получит изменение скорости не 0,09 km/sec, каковое необходимо было для обратного возвращения на землю, а иное, то в зависимости от знака этого изменения он будет удаляться или приближаться к солнцу, описывая вокруг него эллипс. Например, уменьшив скорость на 2,4 km/sec можно заставить снаряд описать эллипс, касательный к орбите Венеры. Для этого потребуется дополнительный взрыв вещества, масса которого равнялась бы 3,65 массы снаряда в этот момент (при С = 2000 m/sec).
Обратное возвращение на землю необходимо согласовать с периодами вращения Земли и Венеры около солнца. Здесь представляются две возможности: 1) или, долетев до орбиты Венеры, превратиться в ее спутника, совершить около нее несколько оборотов и, выждав время, пуститься по дуге эллипса в обратный путь к Земле. На это потребуется 2,15 года полета при отношении начальной и конечной масс снаряда 83000; 2) или, долетев до Венеры, снаряд летит обратно к земной орбите, пересекает ее, летит еще дальше до некоторого места и возвращается обратно по эллипсу, касательному к земной орбите в такой точке, в которой, по расчету, в это время будет находиться земля. На такой полет потребуется 1,58 лет и отношение масс снаряда 82000 (при С =2000 m/sec).
в) Облет Марса аналогичен облету Венеры. Необходимо лишь, на высоте 800000 km над землей не уменьшить, а увеличить скорость полета ракеты. Продолжительность полета будет около 1½ лет и вес снаряда при взлете с земли потребуется (при весе его головки с снаряжением при взлете 16,72 тонны):
при С = 2 km/sec . . . . . . 567000 t
" С = 2,5 " . . . . . . 69500 "
" С = 3 " . . . . . . 17600 "
" С = 4 " . . . . . . 3150 "
" С = 5 " . . . . . . 1130 "
Спуск на другие небесные тела.
а) Спуск на Венеру. Для полета с Земли на Венеру со спуском на нее потребуется 176 дней. Вес снаряда и горючего будет:
Начальный вес головки снаряда (люди, головка, припасы). . . . 7 t .
при спуске на Венеру . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3,5 "
Начальный вес всего снаряда:
С = 2 km/sec . . . . . . . . . . . . . . . . . 54800 t .
С = 2,5 " . . . . . . . . . . . . . . . . . 8800 "
С = 3 " . . . . . . . . . . . . . . . . . 2800 "
С = 4 " . . . . . . . . . . . . . . . . . 620 "
С = 5 " . . . . . . . . . . . . . . . . . 260 "
Если же предвидеть необходимость брать горючее и для обратного возвращения и спуска на землю, то начальный вес ракеты будет:
при С = 2 km sec . . . . . . . . 670000000 t
" С = 2,5 " . . . . . . . . 17000000 "
" С = 3 " . . . . . . . . 1600000 "
" С = 4 " . . . . . . . . 74000 "
" С = 5 " . . . . . . . . 1240 "
б) Спуск на Марс. Полет с Земли со спуском на Марс потребует 265 дней.
Вес головки снаряда при подъеме с земли . . . . . . . . . . . . . . . . 9 t .
" " " " спуске на Марс . . . . . . . . . . . . . . . . 3,2 "
Вес всего снаряда при подъеме с Земли:
| Скорости газов. | Только для полета
на Марс (тонны). | Для полета обратно
(взрывчатые вещества
берутся на Марсе
(тонны). |
| С=2,0 km/sec | 875000 | 1430 |
| С=2,5 " |
76500 | 515 |
| С=3,0 " | 15000 | 265 |
| С=4 " | 2200 | 118 |
| С=5 " | 690 |
71 |
в) Спуск на Луну. Продолжительность полета с Земли на Луну 15 дней.
Начальный вес головки снаряда с запасами . . . . . . . . . . . . . . 2,6 t.
Начальный вес (в тоннах) всего снаряда при взлете с Земли:
Скорость извержения
газов. | Полет только
на Луну. | Полет с Луны на
Землю (взрывчатые
вещества берутся
на Луне). | Полет с Земли на
Луну с запасом
взрывчатых веществ
на Земле. |
| С = 2 km/sec . . . . . . . |
8250 t |
8,9 t |
28000 t |
| С = 2,5 " . . . . . . . |
1610 " |
6,9 " | 4250 " |
| С = 3 " . . . . . . . |
555 " |
5,9 " | 1250 " |
| С = 4 " . . . . . . . |
144 " | 4,8 " |
890 " |
| С = 5 " . . . . . . . |
64 " |
4,3 " |
700 " |
г) Легкость взлета с луны указывает на желательность использования ее, как станции для полета на другие планеты. В нижеследующей таблице даны начальные веса снаряда (в тоннах) при полете с Луны.
Скорость
извержения
газов (С)
km/sec. | Круговой полет
Луна – Венера –
Марс без спуска
на Венеру и Марс.
t. | Полет Луна Марс со
спуском
на Марсе. t. | Полет Луна –
Венера,
со спуском
на Венере.
t | Полет Луна –
Марс со спуском
на Марсе и с запасом на
Луне для
обратного
полета.
t. | Полет Луна –
Венера со
спуском на
Венере и с
запасом на
Луне для
обратного
полета.
t. |
| С = 2,0 | 2070 | 3190 | 200 | 75000 | 290000 |
| С = 2,5 | 780 |
860 | 99 | 11800 | 36300 |
| C = 3 | 417 | 370 | 67 | 3600 | 9900 |
| С = 4 | 194 | 136 | 38 | 850 | 1780 |
| С = 5 | 124 | 76 | 29 | 360 | 680 |
На стр. 204 дано сопоставление результатов, полученных Гоманном.
Результаты подсчетов Эсно-Пельтри.
Эсно-Пельтри в своем сочинении «L'exploration par fusees de la tres haute atmosphere et la possibilite des voyag-es interplanetaires» (Paris, 1927, pg. 29), дает следующие результаты подсчетов для отношения начальной массы аппарата к полезной конечной (M0/P).Ракету он полагает летящей с постоянным ускорением Г и с человеком. Подсчеты он делает для трех случаев Г и сначала получает высоты у c скорость на этой высоте vc и время полета tc. Форму аппарата он полагает с коэффициентами сопротивления ее (k) разными.
Для разных скоростей извержения v и для разных Г он дает ,таблицу M 0/ P
| Г | k | у c km | vc m/sec |
t c sec |
| 10 g | 0,1 | 637 | 10660 | 120 |
| 2 g | 0,5 | 3185 | 9133 | 750 |
| 1,1 g | 0,91 | 5800 | 8080 | 36 м. 40 с. |
| v m/sec |
Г = 1,1 g |
Г = 2 g |
Г = 10 g |
| 2000 | 143000 | 1574 | 358,5 |
| 2500 | 13270 | 361,3 | 110,6 |
| 3000 | 2700 | 135,2 | 50,5 |
| 3500 | 883 | 67,1 | 28,8 |
| 4000 | 378 | 39,7 | 18,9 |
| 4500 | 196 | 26,3 | 13,6 |
| 5000 | 115 | 19,1 | 10,5 |
| 6000 | 52,2 | 11,6 | 7,10 |
| 7000 | 29,7 | 8,19 | 5,37 |
| 8000 | 19,4 | 6.30 | 4,35 |
| 9000 | 14,0 | 5.13 | 3,69 |
| 10000 | 10,7 | 4,36 | 3,24 |
Г. Сенфтлебен (Н. A. Senftleben) в журнале «Z. F. М.» (1928, st. 319, 367), развивает теорию взлета космической ракеты в среде без атмосферы и определяет условия, при которых полагается минимум расхода горючего.
|