|
с) Краткая теория ракет.
Ракета движется под влиянием реакции или обратного толчка ею же выбрасываемых газов.
| |
 |
|
| |
Черт. 160. |
Черт. 161. |
|
| |
К теории полета ракеты. |
|
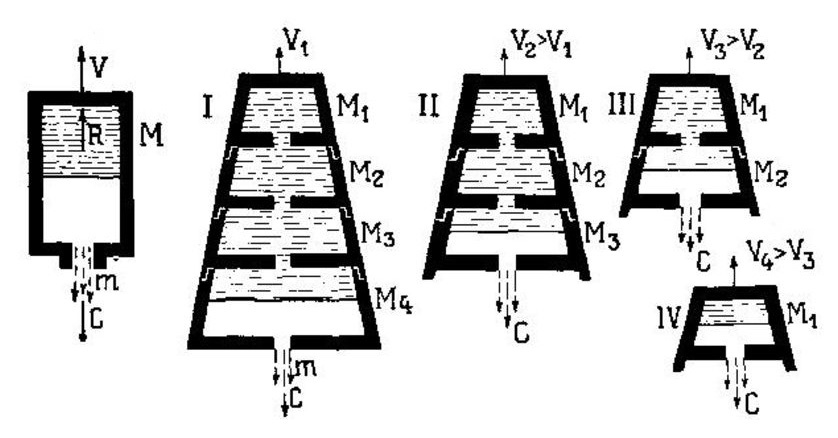
Пусть под влиянием взрыва из ракеты (черт. 160) вырываются в 1 секунду газы, масса которых т, со скоростью с. Под влиянием отдачи R ракета с оставшимся еще не взорвавшимся горючим всею массою M получит скорость v. На основании закона равенства количества движения имеем основное уравнение движения ракеты:
Если предположим, что в секунду вырывается одно и то же количество газов с одинаковой скоростью, то левая часть уравнения (1) будет постоянной, в правой же M, благодаря израсходованию взрывчатого вещества будет уменьшаться, а, следовательно, v должно увеличиваться.
Для большего увеличения скорости v ракеты устраивают ее составной из нескольких частей, которые, по мере сгорания находящегося в ней горючего, постепенно отваливаются, благодаря чему значительно уменьшается остающаяся масса ракеты M и через это увеличивается скорость v.
На черт. 161 изображена такая составная ракета из 4-х частей, массы которых M1, M2, M3, Mi.
В начале движения, когда работает взрывчатое вещество в нижней ее части имеем:
mc = (M1 + M2 + M3 + Mi) v1
Когда же отвалятся части 4-я, 3-я и 2-я, то будем имет...
mc = M1 v4
при чем v4 будет значительно больше v1
На черт. 161 изображены четыре стадии виды ракеты при полном ее виде и постепенном отпадении ее частей.
Чем быстрее ракета удаляется от земли, тем меньше скорость относительно земли извергаемых из нее частиц газа.
| |

Черт. 162. К теории полета ракеты |
|
На черт. 162 схематически изображена картина взаимного отношения скоростей газа и ракеты при подъеме ее от земли. Ракета изображена в пяти положениях. В положении 1-м ее скорость еще равна нулю, газ же развил скорость как по отношению к ракете, так и к земле. В положении 5-м скорость ракеты достигла скорости газов; поэтому vp = v2 Скорость же вырывающегося газа, оставаясь по отношению к ракете равной прежней величине, по отношению земле будет равна нулю, и наблюдателю будет казаться, что облако газа неподвижно висит в воздухе, ракета же уноситься в высоту. В промежуточных положениях скорость ракеты будет от земли постепенно увеличиваться, а скорость газов по отношению к земле постепенно уменьшаться.
Определим зависимость между скоростью (v) ракеты и скоростью (c) газов. Пусть масса ракеты m и она в элемент времени получает приращение скорэсти dv, за счет вырвавшегося газа массы dm.
Тогда, по аналогии с уравнением (1) имеем:
сdm = mdv
откуда
Здесь M0 – начальная масса ракеты, а Mn – конечная.
Из уравнении (2) следует, что если мы желаем сообщить ракете скорость равную n x скорость истечения газов, т. е. чтобы v = nc, то отношение начальной и конечной масс должно удовлетворять равенству
откуда
т. е. отношение начальной и конечной мате ракеты равно п степени
основания (e = 2,71828 =~2,72) натуральных логарифмов. Если ꝏ
n = 1, т. е. v = c, то
т. е. для получения скорости ракеты равной скорости истечения газов,
начальная масса ее должна быть в 2,72 раза больше конечной.
Если
v = 2 с, то M0 = 7,4 M1,
v = 3 с, то M0 = 20,1 M1,
v = 4 с, то M0 = 54,6 M1,
v = 5 с, то M0 = 148,4 M1,
v = 10 с, то M0 = 22026 M1,
v = 30 с, то M0 = 11 биллионов M1. |
Из уравнения 2 го следует, что для ракеты выгодно: 1) увеличивать
возможно более скорость истечения газов: (c) и 2) увеличивать отношение начальной и конечной масс ее (M0 / M1).
Однако, на практике эти числа беспредельно увеличивать нельзя.
Например, если применить в качестве взрывчатого вещества гремучий
газ, то прн скорости его при взрыве даже до 5000 m/sec можно было
бы получить v = 12000 m/sec при M0 / M1 = 12. Но благодаря малому
удельному весу смеси, образующей гремучий газ, ракета должна иметь
большой объем, т. е. или большое поперечное сечение, которое увеличит сопротивление воздуха, или большую длину, что грозит опасностью
ее перелома.
Следует иметь в виду, что требуемую для межпланетных сообщений
скорость ракета может получить быстро, если в ней нет человека, но
при этом следует давать ей наивыгоднейшее ускорение с одной
стороны, чтобы скорее освободиться от земного притяжения, но с другой, не увеличивать чрезмерно сопротивления воздуха. Для ракеты же
с пассажирами следует еще иметь в виду опасность чрезмерного ускорения для человека. Это ускорение не должно превышать 40 m/sec2.
Макс Валье дает следующие цифры для межпланетной ракеты:
1. Для полета от Земли до границы солнечной системы:
c = 4000 m/sec, v = 19000 m/sec; ракета составная. При отлете от
Земли до границы земного притяжения M0/M1 = 12,1; далее часть оболочки отпадает и отношение оставшихся масс делается M1/M1' = 43,1.
2. Для полета на Юпитер:
v = 172 c.; M0/M1 = 4,7 триллионов.
3. Для полета на Марс: горючего необходимо в 1½ раза больше, чем для полета на Луну.
Проследим параллель между ядром, вылетающим из жерла пушки и ракетой.
Первое, имея наивысшую скорость при выходе из жерла, постепенно эту скорость теряет. Вторая же может получить при помощи взрывов любую скорость в известных пределах. Вначале, в низких слоях атмосферы, где сопротивление воздуха велико, она может двигаться медленно, чтобы не затрачивать много горючего, выше же, где плотность воздуха мала, она должна развивать большую скорость. Следует однако иметь в виду, что выгодно вообще сообщать ракете как можно большую скорость подъема и возможно скорее уйти из сферы земного притяжения, так как каждая секунда замедления отражается на непроизводительной затрате энергии горючего на поддержание ракеты в пространстве.
Оберт старается согласовать оба вышеупомянутые требования путем выбора так называемой наивыгоднейшей скорости, которой ракета должна придерживаться в каждый данный момент, пока она находится в пределах атмосферы, определяя ее из условия минимума затраты горючего.
| |
Черт. 163. К теории полета ракеты |
|
В случае устройства пассажирской ракеты полет ее необходимо огра- ничить условием, чтобы ускорение не превышало того, которое еще он может переносить и которое равно около 30 m/sec2 (иногда даже до 45 m/sec2).
Так как при поднимании отвесно вверх ускорение движения складывается с имеющимся уже ускорением силы тяжести (9,81 m/sec2) то при таком подъеме безопасным ускорением движения будет лишь 30-9,81 = 20,19 m/sec2.
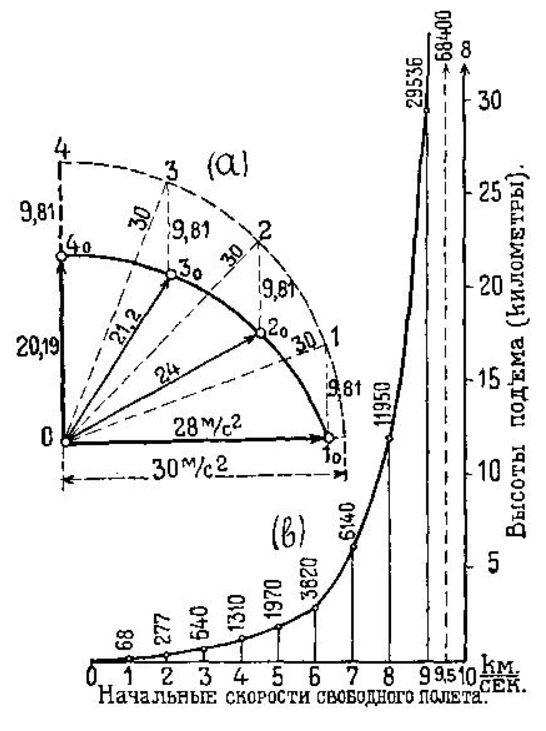
Поэтому, для получения большей безопасности скорости полета выгоднее сначала лететь не по отвесу, а наклонно. На черт. 163 а показано влияние углов наклона на испытываемое человеком ускорение. Последнее на диаграмме принято 30 m/sec2.
При полете при горизонтали (010) можно развить ускорение в 28 m/sec2, которое вместе с g = 9.81 дает безопасное 30 m/sec2.
При полете по направлению 020 можно дать ускорение 24 m/sec; по направлению 030 – 21,2 m/sec.
Можно подсчитать, до какой высоты долетит ракета, если сначала будет иметь ускорение в 30 m/sec до тех пор, пока не достигнет некоторой скорости v1, а затем, считая эту скорость за начальную скорость свободного полета определить еще и остальную высоту полета до точки, откуда она начнет падать на землю.
| |

Черт. 164. К теории полета ракеты и ядра |
|
Например, полагая скорость начала свободного (без взрывов) полета v1 = 1000 m/sec имеем:
1, Путь от земли (v1 = 0) до высоты, где v1 = 1000 m/sec, равен:
h1 = ½ • 30 • t2, где t определяется по формуле: 1000 = 30 t;
| h1 |
|
= |
|
½ • 30 • |
|
10002 |
|
= |
|
16666 m |
|
= |
|
16.666 km. |
|
| |
|
302 |
|
|
|
|
2. Высота же (h2) свободного полета (считая приблизительно на высоте g1 равным 9,81), получится
| h2 |
|
= |
|
v |
|
= |
|
10002 |
|
= |
|
50,9 km. |
|
| |
|
2g |
2 • 9,81 |
|
|
Полная высота будет H = h1 + h2 = 16,666 + 50,9 =~ 68 km.
Черт. 163b изображает результаты подобных подсчетов, сделанных для полета ракеты при начальных скоростях свободного (без взрывов) ее полета от v1 = 1 km/sec, до v = 10 km/sec.
Ординаты кривой показывают высоты (в km), которых может достичь ракета. Для больших высот h1, ускорение g следует определять по формуле
| |
Черт. 165. С пуск ракеты
с торможением |
|
На черт. 164 изображено (по М. Вальеру) сравнение двух полетов: ракеты (линия ABC) и ядра из пушки CBE – с участием на участке CB – сопротивления воздуха, и DBE – без – учета сопротивления воздуха.
По оси ординат отложены скорости подъема в m/sec, а по оси абсцисс – удаления тела от поверхности земли в земных радиусах.
Ракета сначала поднимается с земли с равномерным ускорением 30 m/sec, пока скорость ее не достигнет vb — 10000 m/sec; это будет на высоте h1 определяемой по тем же формулам, что и выше, именно:
h1 = ½ • 30 t2; t = 10000 / 30 = 333 сек.;
h1 = ½ • 30 • 100002 / 302 = 1666,6 km =~ ¼ земного радиуса.
Эта высота и скорость дают на диаграмме точку B. Далее ракета летит свободным полетом с постепенно убывающей скоростью. Например, на высоте h2 = r (от поверхности земли) скорость определится по формуле:
| v22 |
|
= |
|
v12 – 2g1h12 |
|
( |
|
1 |
– |
1 |
) |
. |
| |
h1 |
2r |
| здесь |
|
g |
|
= |
|
9,81 • r2 |
|
= |
|
6,28 m/sec2; |
| |
(r + ¼ r) |
h1 = 6371 + 1666,6 =~ 8037 km; 2r = 6371x2 = 12742 km.
Подставляя эти значения, получим:
| v22 |
|
= |
|
100002 – 2 • 6,28 • 8037 |
|
( |
|
1 |
– |
1 |
) |
|
=~ |
|
8000 km. |
| 8037 |
12742 |
что и дает точку Е на диаграмме.
Кривая EB, продолженная влево, дает на оси ординат точку, определяющую скорость вылета ядра из жерла пушки для подобного же полета. Однако, учитывая сопротивление воздуха, придется увеличить начальную скорость ядра на величину DC, дав ядру начальную скорость около 12000 m/sec.
Ракетный аппарат с тормозящей реакцией.
Спуск на небесное тело, не обладающее атмосферой, например, на Луну, возможен лишь при помощи реакции вырывающихся газов, тормозящих этот спуск.
| |

Черт. 166. М. Вальер. |
|
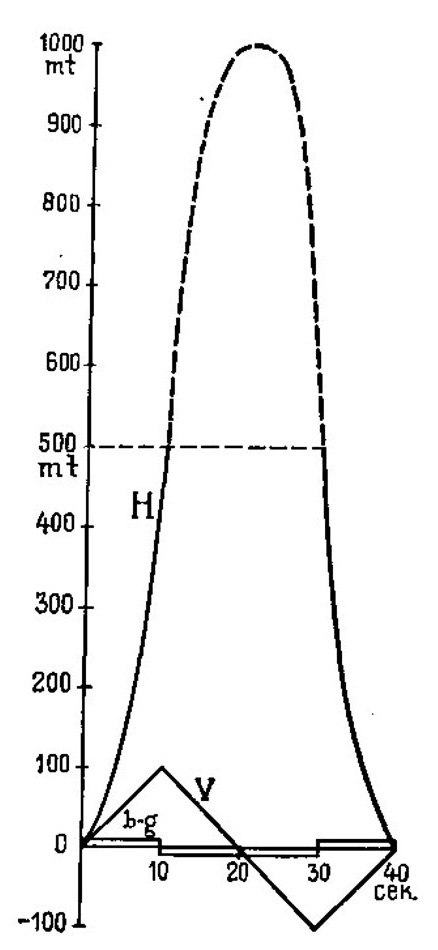
Для выяснения характера этого торможения на прилагаемом чертеже 165 изображен простейший случай взлета и спуска ракетного аппарата с человеком, поднимающегося с земли на высоту 1000 m. и спускающегося обратно с торможением. В нем две ракеты – одна для подъема, другая для спуска. Продолжительность горения каждой – 10 сек. Развиваемое ускорение при взрывах = 2 g. Вес всего горючего (порох) – 40 kg. Сначала, в течение 10 сек.
происходит подъем до высоты H = 1/2 . 10 . 102 = 500 m. Затем – замедленный полет в течение 10 сек. до высоты Н = 1000 m. Далее, свободное падение до высоты 500 m (10 сек.) и, наконец, торможение до земли (10 с.). Соответственные ускорения будут: b – g = 1) 2g – g = +g, 2) 0 – g = –g; 3) 0 – g = –g; 4) 2g – g = +g. На чертеже изменение ускорений показано ступенчатой линией. Скорость определяется формулой: v = (b – g)t; и ее изменение изображается ломаной линией (v = 0 при t = 0,20 и 40 сек.). Высота подъема изображена кривой линией.
|