|
Глава IV
Характеристики ракетных двигателей и аппаратов

Компоненты топлива (горючее и окислитель) поступают в камеру двигателя, воспламеняются и получившиеся продукты сгорания с большой скоростью вытекают через сопло, в результате чего двигатель дает силу тяги, равную реакции струи вытекающих газов.
Таким образом тепловая энергия топлива непосредственно преобразуется в живую силу, которая может быть использована для совершения полезной работы. Тяга ракетного двигателя равна секундному количеству движения струи:
Ф = m • W,
Ф – тяга двигателя,
k/g – секундная масса,
k – секундный расход горючей смеси,
g – земное ускорение,
W – скорость истечения газов из сопла.
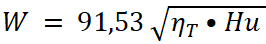 , , |
где:
ηT = 0,2 + 0,4 – термический коэфициент полезного действия.
Hu – теплотворная способность 1 кг горючей смеси, составленной из топлива и окислителя в соответствующей пропорции.
С подъемом на высоту плотность воздуха уменьшается, а следовательно разность давлений в камере сгорания двигателя и в окружающей внешней среде увеличивается. Благодаря этому тяга двигателя Ф с подъемом возрастает.
На рис. И изображен характер изменения тяги небольшого ракетного двигателя. По вертикальной оси отложены величины Ф в килограммах, а по горизонтальной – высоты в тысячах метров. Из диаграммы видно, что прирост тяги на высоте около 20 км составит примерно 8%.
На рис. 12 показана зависимость силы тяги от секундного расхода смеси, что, как мы видели из выражения для Ф, является одним из основных условий. Тем больше секундный расход, тем большую реактивную силу может дать двигатель.
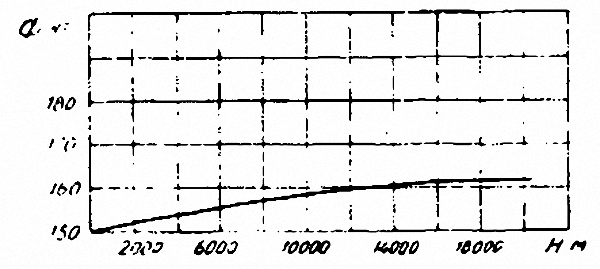
Рис. 11. Изменение тяги с высотой. |
Другим фактором, сильно влияющим на величину реактивной силы, является скорость истечения продуктов сгорания. Для увеличения полезной отдачи двигателя необходимо стремиться путем выбора соответствующего состава смеси к наибольшему значению W.
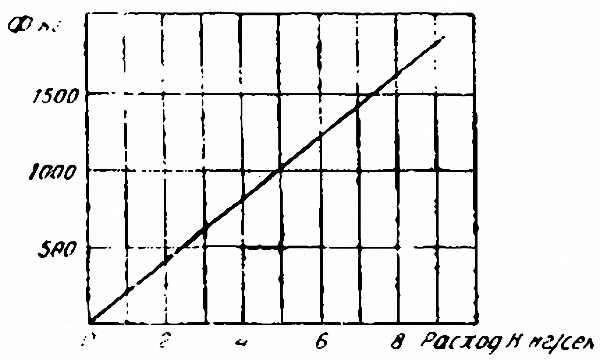
Рис. 12. Изменение расхода по тяге. |
Коэфициент полезного действия ракеты может быть представлен в следующем виде:
где :
V – скорость полета,
W – скорость истечения.
На рис. 13 изображена зависимость коэфициента полезного действия ракеты от скорости полета, вычисленная для значения W = 2400 м/сек.
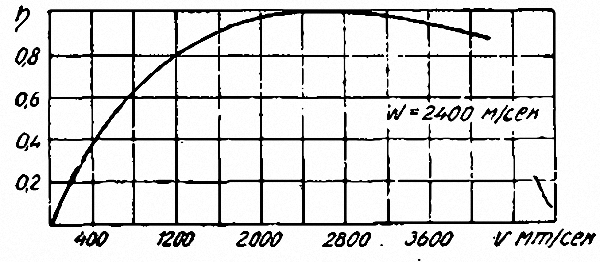
Рис. 13. Кривая коэфициента полезного действия. |
По горизонтальной оси диаграммы отложены величины V, а по вертикальной – ηP. Из диаграммы (рис. 13) ясно видно, насколько невыгодным будет использование ракетного двигателя на малых скоростях движения, что как раз имеет место при полетах у земли и у всякого рода ракетных автомобилей и тому подобных аппаратов. Стремление многих изобретателей использовать ракетные моторы на малых земных скоростях свидетельствует об их полной неграмотности.
Далее при расчете ракетного аппарата немаловажным условием является правильный выбор продолжительности горения мотора. Может случиться так, что, стремясь к достижению наилучших результатов, в ракету будет налито такое количество смеси, которое все равно ье будет полезно использовано. Время горения может быть тем больше, чем больше отношение веса горючего к полному весу ракеты и чем больше скорость истечения продуктов сгорания. Характер этой зависимости от W показан на рис. 14, где по вертикальной оси отложены различные значения скорости а по горизонтальной – время в минутах.
Тяга воздушного ракетного мотора может быть рассчитана по следующей формуле:
где принято:
Сф – коэфициент тяги,
а – площадь входного сечения двигателя, Δ – плотность воздуха,
V – скорость движения.
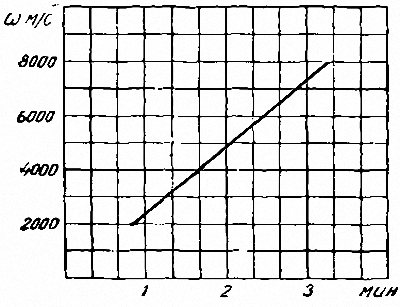
Рис. 14. Время горения. |
Подбор и расчет элементов ракетных моторов и установок во многих случаях могут быть произведены известными приемами, употребляющимися в других соответствующих областях техники. Однако необходимо отметить, что конечный результат и достижение на практике удовлетворительной работы ракетной моторной установки могут быть получены только путем эксперимента и тщательного изучения работы двигателя в стационарных и лабораторных условиях.
Необычайная простота даже известная схематичность ракетных устройств не должны служить поводом к излишнему легкомыслию при работах в этой области.
Полет всякого ракетного летательного аппарата (РЛА) может быть разделен на ряд этапов. Первый – отрыв от земли и взлет, причем последний может быть произведен при помощи каких-либо приспособлений. Далее РЛА вступает во второй этап – полет вверх с все увеличивающейся скоростью и с работающим ракетным мотором. Такой полет может происходить как по вертикали вверх, так и под углом к горизонту. При этом бескрылый РЛА будет иметь некоторую криволинейную траекторию, а РЛА с крыльями благодаря все увеличивающейся скорости полета и все большей и большей подъемной силе будет стремиться увеличить угол взлета и затем перейти на мертвую петлю. Поэтому в последнем случае, если действительно скорость взлета будет велика, необходимо устройство такого приспособления или управления для пилота, посредством которого аппарату была бы придана способность выдерживать прямолинейную траекторию набора высоты.
По окончании горения мотора, когда реактивная сила больше уже на РЛА не действует, последний продолжает свой полет вверх по инерции. Как будет видно из последующего изложения, длина пути, проходимого по инерции, без мотора, может составить очень большую величину, в несколько раз превосходящую путь, ройденный с мотором.
Достигнув наивысшей точки, ракета переходит в свободное падение к земле. Если аппарат имеет крылья, то с достигнутой высоты он планирует. В общем виде уравнения движения могут быть представлены так:
Здесь;
V – скорость полета,
θ – угол наклона траектории,
Ф – сила тяги мотора,
m – масса аппарата,
Δ – плотность среды,
g – земное ускорение,
Rx, Rv – аэродинамические силы для скорости единицы.
Известными1 методами численного интегрирования, решив уравнения, можно найти по времени все интересующие нас данные РЛА и построить его траекторию. Приближенными способами, сделав ряд допущений, можно найти основные интересующие нас характеристики ракетных летательных аппаратов.
____________________________
1 В задачу этой книги не входило подробное изложение расчетов РЛА, поэтому всех интересующихся отсылаем к специальным работам.
В случае прямолинейной траектории полета с мотором под углом в к горизонту уравнение равновесия всех сил напишется так:
RxV12 = Ф – Qcp sin θ,
где:
Rx = CxСΔS - составляющая вредного сопротивления.
Qcp – средний вес аппарата (берем его проекцию на траекторию).
будет наибольшей скоростью РЛА.
В случае вертикального подъема sin θ = 1 и
Полученное значение скорости будет средним, в случае если при расчете брался средний вес за время от момента старта и до конца горения.
Высота подъема с мотором будет:
где t – время действия мотора.
Для того чтобы учесть изменение плотности, можно, найдя высоту Z1 взяв соответствующую ей Δ, пересчитать снова значение V:
и высота подъема с мотором будет:
Для ракеты в случае вертикального подъема, ведя расчет без учета сопротивления воздуха, можно написать выражение для наибольшей скорости полета так:
Qполн. – полетный вес в момент старта,
Qпуст. – вес пустого аппарата,
t – время горения.
Высота подъема с мотором будет:
Высота подъема при полете по инерции
и полная наибольшая высота подъема
Если произвести расчет с учетом сопротивления воздуха, то полученные данные значительно изменятся в сторону ухудшения, причем для низко летающих ракет разница будет больше, чем для ракет с большим потолком. В качестве примера на рис. 15 приведены две траектории полета под углом одной и той же ракеты с учетом сопротивления воздуха и без него.

Рис. 15. Сравнение траекторий. |
На рис. 16 показаны характеристики (с учетом сопротивления воздуха) для ракеты, достигающей высоты полета 133 км. По горизонтальной оси отложено время в секундах, а по вертикальной – величины ускорения j, скорости V и высоты Z в каждый данный момент полета. Продолжительность последнего составляет 233 секунды.
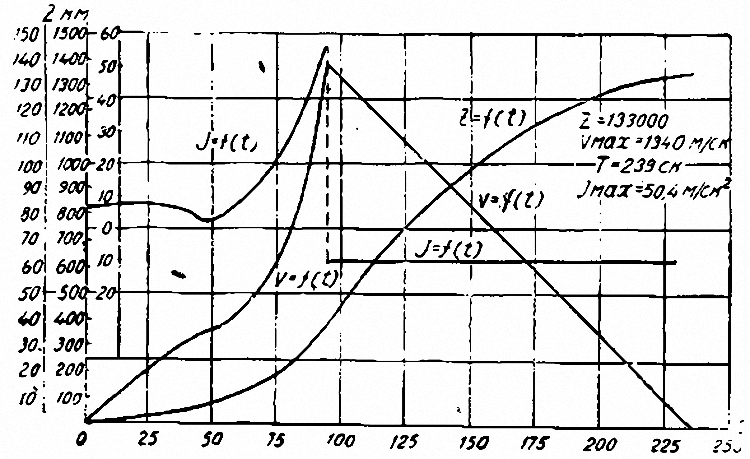
Рис. 16. Характеристики ракеты. |
Скорость полета быстро возрастает, достигая на 25-й секунде 220 м/сек, на 50-й превышая 350 м/сек. После этого благодаря тому, что ракета оказывается на высоте 90 км, где сопротивление полету ничтожно, скорость увеличивается еще быстрее и достигает своего максимума в 1340 м/сек на высоте около 100 км. Далее полет происходит по инерции до высоты 133 км, на которой теоретически скорость падает до нуля и аппарат переходит на спуск. Ускорение сначала несколько уменьшается, кривая его в момент перехода ракетной звуковой скорости делает изгиб и затем круто растет вверх.
В заключение необходимо указать, что работы над ракетными моторами и аппаратами являются новой, мало изученной областью техники, и понятно, что немногие известные и заслуживающие внимания теоретические методы для предварительного определения характеристик нуждаются в дальнейшей доработке и в серьезной проверке на практике.

|